Physique BCPST
DIFFUSION PARTICULAIRE | LOI DE FICK
Extrait du sujet 2024 AGRO-VETO voir le sujet corrigé complet
III. L’oxygénation du sang dans les capillaires pulmonaires.
Le bon fonctionnement des organes nécessite un apport en dioxygène régulier. Dans cette partie on propose d’étudier l’oxygénation du sang dans les capillaires pulmonaires.
On aborde l’oxygénation du sang par une approche de diffusion de particules. Dans un souci de simplification, plusieurs processus ne sont pas pris en compte comme la capture du dioxygène par les globules rouges ou bien le transport de dioxygène par convection dans les capillaires pulmonaires.
A. Modèle unidimensionnel en régime stationnaire.
On se propose d’établir l’équation de la diffusion concernant la concentration en dioxygène $O_2$ dans un capillaire pulmonaire. On néglige le transport du dioxygène par convection dans les capillaires sanguins.
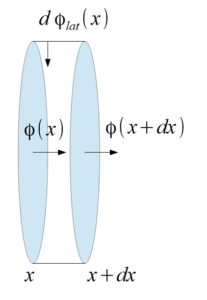
On s’intéresse à un capillaire pulmonaire assimilable à un tube cylindrique (de rayon $𝑎$ et de longueur $𝐿$) d’axe $𝑥$ caractérisé par une concentration en dioxygène $𝐶_{O_2}(𝑥)$ (voir schéma figure 9 ci-contre). La concentration en dioxygène est supposée uniforme sur toute section du cylindre orthogonale à $𝑂𝑥$.
On considère le régime stationnaire. On note $𝐶_{O_2}(𝑥 = 0) = 𝐶_1$ la concentration molaire en $O_2$ à l’entrée du capillaire et $𝐶_{O_2}(𝑥 = 𝐿) = 𝐶_2$ la concentration molaire à la sortie du capillaire. On note $Φ(𝑥)$ le flux algébrique de $O_2$ rentrant en $𝑥$ dans le sens de $\vec{𝑢_𝑥}$.
Pour tenir compte de l’apport de molécules de $O_2$ par diffusion à travers la membrane alvéolo-capillaire on considère un flux latéral de particules.
Le flux latéral de particules entrant par une surface latérale de cylindre $d𝑆_{lat} = 𝜋𝑎d𝑥$ s’exprime par $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ où $𝐶_{ext}$ est la concentration en dioxygène dans l’alvéole pulmonaire et $ℎ$ est la perméabilité de la membrane alvéolo-capillaire. Cet apport latéral se fait sur la moitié supérieure de la surface latérale du cylindre.
$𝐶_{ext}$ est supposée constante. Le capillaire est suffisamment long pour considérer que $𝐶_{ext} = 𝐶_2 > 𝐶_1$.
On choisit d’exprimer toutes les concentrations en $mol.m^{−3}$ et tous les flux en $mol.s^{−1}$.
20.Préciser l’unité de $ℎ$ en fonction des unités de base du système international.
$dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ soit : $h = \frac{d \Phi_{lat}}{[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}}$ $=\frac{[mol].[s]^{-1}}{[mol].[m]^{-3}.[m]^2}$ $=\frac{[m]}{[s]}$
21.En faisant un bilan de particules sur une tranche de cylindre comprise entre $𝑥$ et $𝑥 + d𝑥$, montrer que le flux $Φ(𝑥)$ suit l’équation différentielle suivante : $\frac{dΦ}{d𝑥} = 𝜋𝑎ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]$
Nous travaillons sur un élément de volume représenté ci-dessous :
En faisant un bilan particulaire des flux et en prenant $\Phi(x)$ comme étant le flux entrant et $\Phi(x+dx)$ le flux sortant, on obtient :
$\Phi(x) – \Phi(x+dx) + d\Phi_{lat} =0$ $\Rightarrow$ $- \frac{d \Phi(x)}{dx}dx + h [C_{ext} – C_{O_2} (x)]dS_{lat} =0$ $\Rightarrow$ $-\frac{d\Phi(x)}{dx} dx + h [C_{ext} – C_{O_2} (x)]\pi a dx = 0$ $\Rightarrow$ $\frac{d\Phi(x)}{dx}= \pi a h [C_{ext} – C_{O_2} (x)]$
22.Rappeler la loi de Fick. En déduire une relation entre $Φ(𝑥)$ et $𝐶_{O_2}(𝑥)$. On notera $𝐷_{O_2}$ le coefficient de diffusion du dioxygène dans le sang et on exprimera l’unité de $𝐷_{O_2}$ en fonction des unités de base du système international.
Loi de Fick : $\Phi(x)= – D_{O_2} \times S \times \frac{dC}{dx}$, ce qui donne par dérivation :
$\frac{d \Phi(x)}{dx} = – D_{O_2} \times S \times \frac{d^2C}{dx^2}$
Unité de $ D_{O_2}$ :
$ D_{O_2} = \frac{\Phi \times dx}{dC \times S} =\frac{[mol].[s]^{-1} .[m]}{[mol].[m]^{-3} [m]^2} $$=\frac{[m]^2}{[s]}$
23.En déduire que l’équation différentielle vérifiée par $𝐶_{O_2}(𝑥)$ peut se mettre sous la forme suivante :
$\frac{d^2 𝐶_{O_2}}{d𝑥^2} − \frac{𝐶_{O_2}(𝑥) − 𝐶_{ext}}{ℓ^2} = 0$ avec $ℓ^2 = \frac{𝐷_{O_2}𝑎}{ℎ}$
Faire l’application numérique pour $ℓ$ et donner un sens physique à ce paramètre.
Données :
▷ Rayon typique d’un capillaire pulmonaire : $𝑎 = 4,0 μm$
▷ Perméabilité de la membrane alvéolo-capillaire : $ℎ = 66 × 10^{−6} unités SI$
▷ Coefficient de diffusion de $O_2$ dans le sang : $𝐷_{O_2} = 1,7 × 10^{−7} unités SI$
$\frac{d \Phi(x)}{dx} = – D_{O_2} \times S \times \frac{d^2C}{dx^2}$
Or, $\frac{d \Phi(x)}{dx} =\pi a h [C_{ext} – CO_2 (x)]$ $\Rightarrow$ $- D_{O_2} \times S \times \frac{d^2C}{dx^2} = \pi a h [C_{ext} – CO_2 (x)]$ $\Rightarrow$ $D_{O_2} S \frac{d^2C}{dx^2} + \pi a h [C_{ext} – CO_2 (x)]=0$ $\Rightarrow$ $\frac{d^2C}{dx^2} + \frac{\pi a h}{D_{O_2} S}[C_{ext} – CO_2 (x)] = 0$
$S = \pi a^2$ $\Rightarrow$ $\frac{d^2C}{dx^2} + \frac{[C_{ext} – CO_2 (x)]}{l^2} = 0$, avec $l^2 = \frac{D_{O_2} a}{h}$
Application Numérique :
$l = \sqrt{\frac{1,7.10^{-7} \times 4.10^{-6}}{66.10^{-6}}}= 5,1.10^{-5}m$ avec l homogène à une distance et représentant la distance de diffusion pour le régime permanent.
24.La solution de l’équation différentielle de la question 23. peut s’écrire sous la forme suivante :
$𝐶_{O_2}(𝑥) = 𝐴 + 𝐵e^{−𝑥/ℓ} + 𝐶e^{𝑥/ℓ}$
a.La longueur d’un capillaire pulmonaire $𝐿$ est typiquement de 1 mm. En comparant $ℓ$ et $𝐿$, expliquer succinctement que l’on puisse considérer que $𝐿 = +∞$ dans la suite.
$l \simeq 10^{-5}$ et $L \simeq 10^{-3}$, donc $l<<L$, on peut alors considérer que $L = + \infty$
b.Déterminer les constantes $𝐴$, $𝐵$ et $𝐶$ en fonction des données de l’énoncé
Les conditions limites sont : $C_{O_2} (x=0) = C_1$ et $C_{O_2} (x=L) = C_2$
$C_{O_2} (x=0) = A+B+C = C_1$
$C_{O_2} (x=L) =A+ Be^{-\infty} + Ce^{+\infty} = C_2$ ce qui implique $C = 0$(pour ne pas que la solution diverge) et $A=C_2$
Or, $A+B+C = C_1$ $\Rightarrow$ $B=C_1 – C_2$
Au final :
$C_{O_2}(x)= C_2 + (C_1 – C_2)e^{- \frac{x}{l}}$
c.Tracer l’allure de $𝐶_{O_2}(𝑥)$ et faire apparaître $ℓ$ sur votre graphique.
25. Montrer que la quantité de dioxygène transférée par unité de temps de l’alvéole pulmonaire vers le capillaire pulmonaire s’exprime, en moles par seconde, par la relation : $Φ_{lat,1 capillaire} = ℎ (𝐶_{ext} − 𝐶_1) × 𝜋𝑎$
Le flux latéral s’exprime par : $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ $\Rightarrow$ $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]\pi a dx$ , nous connaissons maintenant l’expression de $C_{O_2}(x)$
$\Rightarrow$ $dΦ_{lat} = ℎ[𝐶_{ext} −(C_2-(C_1 – C_2)e^{- \frac{x}{l}})]\pi a dx$, de plus $C_2 = C_{ext} $
$\Rightarrow$ $dΦ_{lat} = ℎ[(C_2 – C_1)e^{- \frac{x}{l}})]\pi a dx$
$\Rightarrow$ $\int dΦ_{lat} = \int_0^L ℎ[(C_2 – C_1)e^{- \frac{x}{l}})]\pi a dx$
$\Rightarrow$ $Φ_{lat,1 capillaire} = \int_0^L ℎ \pi a ((C_2 – C_1)e^{- \frac{x}{l}})) dx$
$\Rightarrow$ $Φ_{lat,1 capillaire} = ℎ \pi a [((C_2 – C_1)\times ( -l e^{- \frac{x}{l}})))]_0^L$
$\Rightarrow$ $Φ_{lat,1 capillaire} =-l ℎ \pi a (C_2 – C_1) ( e^{- \frac{L}{l}} – e^{- \frac{0}{l}} )))]$
$\Rightarrow$ $Φ_{lat,1 capillaire} =-l ℎ \pi a (C_2 – C_1) ( – 1 )))]$
$\Rightarrow$ $Φ_{lat,1 capillaire} =l ℎ \pi a (C_{ext} – C_1)))]$
B. Estimation de la consommation d’oxygène
En pratique, les données d’oxygénation du sang dans les capillaires pulmonaires ne sont pas données en terme de concentration en $mol.m^{−3}$ mais en terme de pression partielle de dioxygène $𝑃_{O_2}$ en mmHg.
Afin de pouvoir comparer des données réelles aux résultats de la partie précédente, nous avons besoin d’introduire le coefficient de Henry $𝜎$ tel que $𝐶_{O_2} = 𝜎 × 𝑃_{O_2}$
Pour le dioxygène dans le sang, on prendra $𝜎 = 1,7 × 10^{−3} mol.m^{−3}.mmHg^{−1}$
Ainsi, la quantité de dioxygène transférée par unité de temps (en $mol·s^{−1}$) de l’alvéole pulmonaire vers le capillaire pulmonaire (voir question 25.) s’exprime en fonction des pressions partielles sous la forme suivante :
$Φ_{lat,1 capillaire} = ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
avec $𝑃_{O_2,ext}$ la pression partielle en dioxygène dans une alvéole pulmonaire et $𝑃_{O2,1}$ la pression partielle en dioxygène à l’entrée d’un capillaire pulmonaire.
En prenant en compte qu’il y a $𝑁$ capillaires pulmonaires placés en parallèle qui permettent l’oxygénation du sang, la quantité de dioxygène transférée par unité de temps (en $mol·s^{−1}$) vers tous les capillaires pulmonaires s’exprime par :
$Φ_{lat,𝑁 capillaires} = 𝑁 × Φ_{lat,1 capillaire} = 𝑁 × ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
26. Déterminer le volume molaire $𝑉_𝑚$ d’un gaz parfait à $25 °C$ sous pression atmosphérique $𝑃_{atm} = 1,013 bar$.
Donnée : Constante des gaz parfaits : $𝑅 = 8,314 J.mol^{−1}.K^{−1}$
$V_m = \frac{V}{N} = \frac{RT}{P}$
Application Numérique :
$V_m = \frac{8,314 \times (25+273)}{1,013.10^5} = 2,44.10^{-2} m^3 .mol^{-1}$
On souhaite estimer le volume de dioxygène transféré par minute des alvéoles-pulmonaires vers les capillaires sanguins en utilisant le modèle développé dans cette partie III.
Pour un individu adulte au repos, le nombre de capillaires pulmonaires fonctionnels est de $𝑁 ≃ 20 × 10^9$ et les pressions partielles en dioxygène sont $𝑃_{O_2,ext} = 100 mmHg$ et $𝑃_{O_2,1} = 40 mmHg$.
27.Déterminer le volume de dioxygène transféré par minute des poumons vers les capillaires pulmonaires. On notera $𝑉_{O_2}$ cette quantité et on l’exprimera en $L.min^{−1}$.
Données :
▷ Rayon typique d’un capillaire pulmonaire : $𝑎 = 4,0 μm$
▷ Perméabilité de la membrane alvéolo-capillaire : $ℎ = 66 × 10^{−6} unités SI$
▷ Coefficient de Henry : $𝜎 = 1,7 × 10^{−3} mol.m^{−3}.mmHg^{−1}$
Pour connaitre le volume de dioxygène transféré il faut repartir de la formule du flux qui nous donne le flux de dioxygène en $mol.s^{-1}$ :
$Φ_{lat,𝑁 capillaires} = 𝑁 × ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
Nous connaissons toute les valeurs, nous pouvons passer à l’application numérique (on peut garder les valeurs de pression en mmHG car le coefficient de Henry est en $mmHg^{-1}$) :
Application Numérique :
$Φ_{lat,𝑁 capillaires} = 20.10^9 \times 66.10^{-6} \times 1,7.10^{-3} \times (100-40) \times \pi \times4.10^{-6} \times 5,1.10^{-5}$ $=8,63.10^{-5} mol.s^{-1}$ , or $V_m=2,4.10^{-2}m^3 . mol^{-1}$, donc :
$Φ_{lat,𝑁 capillaires} = 8,63.10^{-5}\times 2,4.10^{-2}$ $=2,07.10^{-6} m^3 .s^{-1} = 2,07.10^{-3} L.s^{-1}$ $ = 0.12L.min^{-1}$
28.Comparer votre valeur de consommation d’oxygène à la valeur typiquement mesurée pour un individu adulte en bonne santé au repos : $𝑉_{O_2} ≃ 0,2 L.min^{−1}$.
Les valeurs sont du même ordre de grandeur, la différence peut provenir de la valeur de volume molaire prise pour le calcul, en effet, la pression et la température n’est pas égale à celles prises pour le calcul du volume molaire.
Extrait du sujet 2024 G2E voir le sujet corrigé complet
Apparition et croissance des bulles dans le verre par diffusion
Lorsque l’on verse du champagne dans une flûte, une quantité importante de bulles se crée, formant une mousse à la surface libre du liquide. L’expression suivante donne la relation entre la concentration en quantité de matière de dioxyde de carbone dans le champagne et la pression en $Pa$ à la surface libre du champagne dans une situation d’équilibre :
$[CO_2]_{eq} = 0,7 \frac{P}{RT}$
Si la concentration en dioxyde de carbone est supérieure à la concentration d’équilibre $[CO_2]_{eq}$, le liquide est dit sursaturé. La concentration en masse du dioxyde de carbone dans le champagne dans une bouteille fermée est environ égale à $c_c = 12 g.L^{−1}$. On donne la masse molaire du dioxyde de carbone : $𝑀 = 44 g.mol^{−1}$ et la constante des gaz parfaits : $𝑅 = 8,31 J.K^{−1}.mol^{−1}$.
18. Calculer les concentrations en masse du dioxyde de carbone à l’équilibre, à $20 °𝐶$ sous $6 bar$, notée par la suite $𝑐_6$ puis celle à la fin de la détente (conditions ($𝑃_f, 𝑇_f$)), notée $𝑐_f$, et enfin celle à $20 °𝐶$ sous $1 bar$, notée $𝑐_1$. On donnera les valeurs avec deux chiffres significatifs.
Pour calculer directement la concentration en masse, on utilise la formule suivante :
$c = 0,7 \frac{P}{RT} \times \frac{M}{1000}$
pour avoir directement la concentration en $g.L^{-1}$.
Pour $c_6$ :
$c_6 = 0,7 \frac{P}{RT} \times \frac{M}{1000}$
Application Numérique :
$c_6 = 0,7 \frac{6.10^5}{8,31 \times (273+20)} \times \frac{44}{1000}$ $=7,59 g.L^{-1}$
Pour $c_f$ :
Application Numérique :
$c_f = 0,7 \frac{10^5}{8,31 \times 196,9} \times \frac{44}{1000}$ $=1,88 g.L^{-1}$
Pour $c_1$ :
Application Numérique :
$c_1 = 0,7 \frac{10^5}{8,31 \times (273+20)} \times \frac{44}{1000}$ $=1,26 g.L^{-1}$
19. Montrer que les résultats précédents permettent de justifier qu’une détente entraîne a priori la formation de bulles à la surface du liquide.
Quand la bouteille est fermée, le champagne est sursaturé en dioxyde de carbone. Lorsque le bouchon saute et que la pression descend subitement à 1 bar, le dioxyde de carbone se libère en formant un panache de bulle.
Une fois le champagne versé, on observe des chapelets de bulles au sein d’une flute de champagne. L’apparition de ces bulles est principalement due à la présence de fibres de cellulose provenant de particules en suspension dans l’air voire du chiffon utilisé pour essuyer la flûte. Ces fibres de cellulose possèdent une cavité qui renferme de l’air. Les molécules de CO2 dissous en phase aqueuse vont diffuser vers la poche d’air. Celle-ci va grossir jusqu’à atteindre une extrémité de la poche et former alors une bulle.
La pression de l’air dans la poche d’air est prise égale à $1,0 bar$ dans une situation d’équilibre et on se place à $20 °𝐶$.
20. Justifier la diffusion des molécules de $CO_2$ de la phase aqueuse vers la poche d’air.
Réponse
La concentration du $CO_2$ à l’équilibre est $c_c = 12g.L^{-1}$, soit : $c_c = 12 \times \frac{1000}{44} = 272,7 mol.m^{-3}$
Or la concentration de l’air dans les conditions établies dans l’énoncé est :
$C_{air} = \frac{n}{V} = \frac{P}{RT}$
Application Numérique :
$C_{air} = \frac{10^5}{8,31 \times (273+20)} = 41,1mol.m^{-3}$
La concentration du $CO_2$ est donc supérieure à celle de l’air, il y a diffusion de l’élément le plus concentré vers l’élément le moins concentré, donc une diffusion des molécules de $CO_2$ vers la poche d’air.
21. Justifier alors que la poche d’air grossit dans les conditions expérimentales retenues
Réponse
Il y a une augmentation de molécules dans un volume délimité par la fibre de cellulose, la pression va augmenter et ainsi le volume de la poche {air + $CO_2$ } augmentera.
Une fois la bulle formée, elle se détache de la fibre et monte dans le liquide dans lequel elle va grossir. Nous allons étudier cette augmentation de taille. Quand elle se détache de la fibre, la pression au sein de la bulle est égale à 1 bar. La bulle est supposée sphérique de rayon $𝑅_b$.
On considère que la concentration en $CO_2$ dissous vaut $c_c$ loin de la bulle et $𝑐_1$ pour $r = 𝑅_b$. On suppose dans un premier temps que $𝑅_b$ est constant et on se place en régime stationnaire.
22. Justifier qu’un flux $Φ$ de dioxyde de carbone se met en place au sein du champagne liquide et montrer que ce flux se conserve.
Réponse
La différence de concentration dans le champagne (loin de la bulle et sur la surface de la bulle) permet la création d’un flux de dioxyde de carbone des concentrations les plus élevée vers la concentration la moins élevée. Les valeurs $c_c$ et $c_1$ restent constante au fil du temps ce qui a pour conséquence un flux qui se conserve.
23. Donner la loi de Fick dans le contexte étudié en précisant la signification physique des différents termes ainsi que leurs unités. On notera $𝑛^∗(𝑏)$ la concentration particulaire du $CO_2$, $r$ étant la distance au centre de la bulle avec $r > 𝑅_b$ et $𝐷$, le coefficient de diffusion du dioxyde de carbone dans le champagne liquide.
Réponse
Loi de Fick : (attention en coordonnées polaires)
$\Phi = – D \frac{\delta n^*}{\delta r} S$
avec $\Phi$ le flux particulaire traversant une surface S par unité de temps ($s^{-1}$) ; D coefficient de diffusion en $m^2.s^{-1}$ ; $n^*$ densité particulaire $m^{-3}$ ; r en (m) ; S la surface à travers laquelle passe le flux en $m^2$
Dans les questions suivantes, on introduit la constante d’Avogadro $𝒩_a$.
24. Donner la relation entre la concentration en masse de $CO_2$ en solution $𝑐, 𝑛^∗, 𝒩_a$ et la masse molaire $𝑀$ du dioxyde de carbone.
Réponse
On rappelle les formules de base nécessaire :
$n= \frac{N}{N_A}$ ; $M = \frac{m}{n}$ et $n^* = \frac{N}{V}$
Or, $c=\frac{m}{V} = \frac{nM}{V}$ $=\frac{N M}{N_A V} = \frac{n^* M}{N_A}$
25. Montrer que la concentration en masse $𝑐(r)$ au sein du champagne liquide vérifie l’équation : $\frac{𝑑𝑐}{𝑑r} = \frac{A}{4𝜋Dr^2}$, où $𝐴$ est une constante que l’on exprimera en fonction $Φ,𝒩_a et 𝑀$.
Réponse
On a :$\Phi = – D \frac{\delta n^*}{\delta r} S$ (question 23) et $c= \frac{n^* M}{N_A}$ (question 24) soit $n^* = \frac{cN_A}{M}$
$\Rightarrow$ $\Phi = – D \frac{N_A\delta c}{ M \delta r} S$ $\Rightarrow$ $\frac{dc}{dr} = \frac{- \Phi M}{D N_A S}$ avec $S=4\pi r^2$ (surface de la sphère de rayon r à travers laquelle passe le flux)
$\Rightarrow$ $\frac{dc}{dr} = \frac{- \Phi M}{D N_A 4 \pi r^2}$ $=\frac{A}{4\pi D r^2}$ avec $A= \frac{-\Phi M}{N_A}$
26. Établir l’expression suivante de $𝑐(r) : 𝑐(r) = (𝑐_1 − 𝑐_c) \frac{𝑅_b}{r} +𝑐_c$ pour $r > 𝑅_b$.
Réponse
$\frac{dc}{dr} = \frac{A}{4\pi D r^2}$ $\Rightarrow$ $dc = \frac{A}{4\pi D r^2} dr$
Pour retrouver c(r) en fonction de $c_C$ on intègre entre les bornes de rayon r et l’infini
$\int_{c_C}^{c(r) }dc = \frac{A}{4\pi D } \int_{\infty}^r \frac{dr}{r^2}$ $\Rightarrow$ $c(r) -c_C = \frac{A}{4\pi D } [- \frac{1}{r}]_{\infty}^r $ $= \frac{A}{4\pi D } [- \frac{1}{r} + 0]$ donc : $c(r) = -\frac{A}{4\pi D r} + c_C$
Si maintenant on intègre entre les bornes $c_1$ et $c_C$, on obtient :
$\int_{c_1}^{c_C }dc = \frac{A}{4\pi D } \int_{R_b}^{\infty} \frac{dr}{r^2}$ $\Rightarrow$ $c_C – c_1 = \frac{A}{4\pi D } [- \frac{1}{r}]_{R_b}^{\infty} $ $=\frac{A}{4\pi D } \frac{1}{R_b} $ soit : $(c_C – c_1)R_b = \frac{A}{4 \pi D}$
On obtient alors :
$c(r) = -\frac{A}{4\pi D r} + c_C$ $= -(c_C – c_1)\frac{R_b }{ r} + c_C$ $=(c_1 – c_C)\frac{R_b }{ r} + c_C$
Le régime n’est en réalité pas stationnaire. Nous utiliserons néanmoins l’expression trouvée dans la question 26 en prenant en compte le fait que le rayon $𝑅_b(𝑡)$ dépend du temps.
27. En supposant que toutes les molécules de dioxyde de carbone arrivant à la surface de la bulle y pénètrent, montrer que le flux moléculaire, qui s’identifie au taux de variation $Φ = \frac{𝑑𝑁_g}{dt}$ du nombre $𝑁_g$ de molécules de dioxyde de carbone dans la bulle, admet comme expression $\frac{𝑑𝑁_g}{𝑑t} = \frac{𝒩_a 𝑃}{𝑅T} \frac{𝑑V}{dt}$ , où $𝑃 et 𝑇$ sont la pression et la température de la bulle supposées constantes, et $\frac{𝑑V}{dt}$ le taux de variation du volume.
Réponse
Dans la bulle, à chaque instant on a:
$P V(t) = n_g (t) RT$, soit $n_g(t) = \frac{N_g(t)}{N_A}= \frac{P V(t)}{RT}$ $\Rightarrow$ $N_g(t) = \frac{N_A P V(t)}{RT}$ $\Rightarrow$ $\frac{d N_g(t)}{dt } = \frac{P N_A}{RT} \times \frac{dV(t)}{dt}$
28.En déduire la relation : $𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$ dont on vérifiera l’homogénéité.
Réponse
Le flux arrivant dans la bulle depuis le champagne est égal au taux de variation de $CO_2$ dans la bulle car on considère que toutes les molécules de dioxyde de carbone pénètrent.
On a donc : $\frac{dN_g}{dt} = \frac{N_A P}{RT} \frac{dV}{dt} = \frac{D N_A S}{M} \frac{dc}{dr}$ avec $\frac{dc}{dr}=(c_1-c_C)R_b (\frac{-1}{r^2})$ et $V=\frac{4}{3}\pi R_b^3$ soit $\frac{dV}{dt}= 4\pi R_b^2 \frac{d R_b}{dt}$
$\Rightarrow$ $\frac{N_A P}{RT} 4\pi R_b^2 \frac{d R_b}{dt}=\frac{D N_A 4 \pi r^2}{M} (c_1-c_C)R_b (\frac{-1}{r^2}) $ $\Rightarrow$ $𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$
29. On néglige le volume initial de la bulle, de sorte que $𝑅_b(𝑡 = 0) ≈ 0$. En déduire $𝑅_b(𝑡)$.
Réponse
$𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$ $\Rightarrow$ $𝑅_b 𝑑𝑅_b = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇 dt}{𝑃𝑀}$ $\Rightarrow$ $\int_0^{R_b(t)} 𝑅_b 𝑑𝑅_b =\int_0^{t} \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇 dt}{𝑃𝑀}$ $\Rightarrow$ $ [\frac{𝑅_b ^2}{2}]_0^{R_b(t)} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} [t]_0^{t} $ $\Rightarrow$ $ \frac{𝑅_b(t) ^2}{2} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t $ $\Rightarrow$ $ 𝑅_b(t) = \sqrt{2 \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t }$
30. On donne en plus des valeurs numériques précédentes : $𝐷 = 3.10^{−9} 𝑆.𝐼.$ Calculer en $𝑚s$ la durée $∆𝑡$ mise par une bulle pour atteindre un rayon de $10 μm$.
Réponse
$ 𝑅_b(t) = \sqrt{2 \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t }$
Application Numérique :
$R_b(t) = \frac{(10.10^{-6})^2 \times 10^5 \times 44.10^{-3}}{2 \times (12-1,26) \times 3.10^{-9} \times 8,31 \times (273+20)} = 2,8ms$