Physique BCPST
A BCPST | 2024
Sujet corrigé physique A BCPST 2024
L’APPAREIL CARDIOVASCULAIRE
Ce sujet s’intéresse à quelques aspects physiques de l’appareil cardiovasculaire. Après une introduction sur l’appareil cardiovasculaire, le sujet comporte 3 parties indépendantes entre elles (numérotées I à III).
La partie I s’intéresse à la pression artérielle et à sa mesure. La partie II étudie la circulation sanguine en lien avec la loi de Poiseuille. Enfin la partie III présente l’oxygénation du sang dans les capillaires pulmonaires via un modèle fondé sur la diffusion de particules.
Toutes les réponses doivent être dûment justifiées.
Introduction.
L’appareil cardiovasculaire est un système circulatoire en circuit fermé qui assure le transport du sang. Il est constitué du cœur et des vaisseaux sanguins.
On distingue la circulation systémique et la circulation pulmonaire :
— la circulation systémique amène le sang chargé en dioxygène (noté $O_2$ dans la suite du sujet) depuis le cœur gauche jusqu’aux organes puis ramène ce même sang déchargé en $O_2$ mais chargé en dioxyde de carbone (noté $CO_2$ dans la suite du sujet) jusqu’au cœur droit.
— la circulation pulmonaire amène ensuite le sang veineux (sang déchargé en $O_2$ et chargé en $CO_2$) au contact des alvéoles pulmonaires pour le ré-oxygéner puis renvoie ce sang au cœur gauche via la veine pulmonaire.
I. La pression artérielle.
Dans cette partie, on s’intéresse à la mesure de la pression artérielle. Après avoir établi le lien entre le millimètre de mercure (noté mmHg) et le bar (sous-partie A), un dispositif de mesure de pression est présenté (sous-partie B). Enfin, des données de pression artérielle (sous-partie C) sont étudiées.
A. À propos du millimètre de mercure.
En médecine, l’unité encore largement utilisée pour exprimer les pressions est le millimètre de mercure.
On se propose d’établir le lien entre le mmHg et le bar : 760 mmHg = 1,013 bar.
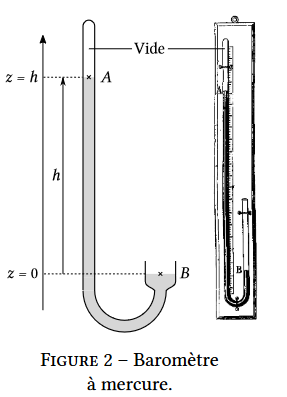
Pour cela, on considère le baromètre à siphon représenté ci-après sur la figure 2.
Ce baromètre utilise du mercure liquide, fluide incompressible de masse volumique $𝜌_Hg = 13,6 × 10^3 kg.m^{−3}$. On note $𝑃_atm = 1,013 bar$ la pression atmosphérique et $𝑔 = 9,81 m⋅s^{−2}$ l’accélération de la pesanteur.
Le point 𝐵 est en contact avec l’atmosphère de sorte que $𝑃_𝐵 = 𝑃_atm$.
On néglige tout phénomène de tension superficielle. De plus, comme la pression de vapeur saturante du mercure est très faible devant la pression atmosphérique, on assimilera l’espace au dessus du point 𝐴 à du vide ; en particulier on considérera que $𝑃_𝐴 ≃ 0 bar$.
1. Rappeler puis établir la relation fondamentale de la statique des fluides dans un fluide de masse volumique $𝜌$ pour un axe $𝑧$ vertical ascendant. Pour la démonstration on pourra postuler que la pression $𝑃$ ne dépend que de la variable $𝑧$, puis écrire l’équilibre d’une couche de fluide comprise entre $𝑧$ et $𝑧 + d𝑧$.
Relation fondamentale de la statique des fluides : $dP = – \rho g dz$ pour un axe z vertical ascendant.
Démonstration :
Soit une couche de fluide comprise entre $z$ et $z +dz$
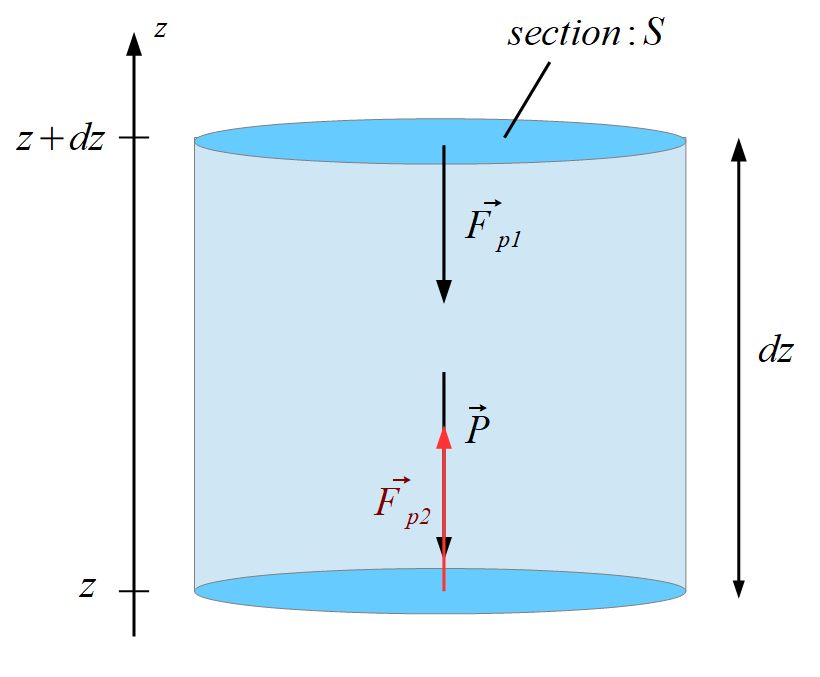
Système d’étude : {couche de fluide élémentaire}
Référentiel terrestre supposé galiléen
2ème loi de Newton :
$\sum \vec F = m \vec a = \vec 0$ car le système est à l’équilibre.
$\Rightarrow$ $\vec P + \vec F_{P1} + \vec F_{P2} = \vec 0$
On projète sur l’axe (Oz) :
$-dm g – F_{P1} + F_{P2} = 0$ $\Rightarrow$ $-P(z+dz) \times S + P(z) \times S = dm g = \rho dV g = \rho dz S g$ $\Rightarrow$ $P(z+dz) – P(z) = dP = – \rho g dz$
2. Établir l’expression de 𝑃(𝑧) dans le mercure liquide.
Dans le mercure : $dP = P(z) – P_A = – \rho_{Hg} g (z – z_A)$ $\Rightarrow$ $P(z) = P_A -\rho_{Hg} g (z – h) $$ = P_A +\rho_{Hg} g ( h-z) $
3. Montrer que la hauteur $ℎ$ de liquide entre les points $𝐴$ et $𝐵$ s’exprime selon $ℎ = \frac{𝑃_{atm}}{𝜌_{Hg}𝑔}.$ Faire l’application numérique de $ℎ$ puis commenter le résultat.
Appliquons le principe de l’hydrostatique entre les points A et B :
$P_A – P_B = – \rho_{Hg} g (z_A – z_B)$ , ici nous avons $P_A \simeq 0$ et $P_B = P_{atm}$ on obtient alors :
$- P_{atm} = – \rho_{Hg} g h$ $\Rightarrow$ $h= \frac{P_{atm}}{\rho_{Hg}g}$
4. Justifier l’utilisation du mercure plutôt que de l’eau liquide pour la réalisation d’un baromètre à siphon.
La hauteur $h$ est inversement proportionnelle à la masse volumique du liquide dans le baromètre. Or la masse volumique de l’eau est environ 14 fois plus faible que celle du mercure. Pour une même variation de pression on aurait alors une différence de hauteur 14 fois plus grande. Au final il faudrait fabriquer un baromètre 14 fois plus grand.
5. Expliquer qualitativement pourquoi les tubes du baromètre ne doivent pas être « trop fins » pour que l’étude précédente soit valable.
Si les tubes étaient plus fins, le liquide à l’intérieur subirait une force de capillarité plus grande. Il faudrait alors prendre en compte cette force dans le bilan des forces ce qui compliquerait le raisonnement.
B. Mesure piézorésistive de pression artérielle.
Afin d’obtenir une mesure de la pression artérielle en continu, la réalisation d’un transducteur de pression est nécessaire. Un transducteur de pression convertit un signal de pression 𝑃(𝑡) en une tension électrique directement mesurable $𝑢_{mes(𝑡)}$.
Un transducteur de pression largement utilisé dans le domaine de la santé exploite le phénomène de piézorésistivité. La piézorésistivité traduit le fait que la résistance électrique de certains matériaux varie selon la pression à laquelle ils sont soumis. Cette dépendance n’est pas due aux variations des caractéristiques géométriques du matériau.
Aucune connaissance sur la piézorésistivité n’est nécessaire pour traiter les questions de cette partie.
On considère un matériau piézorésistif dont la résistance dépend de la pression sous la forme suivante :
$𝑅 = 𝑅_0 [1 + 𝑘(𝑃 − 𝑃_{atm})]$
$𝑃_{atm} = 1,013 bar$ est la pression atmosphérique, $𝑘$ une constante appelée coefficient de piézorésistivité et $𝑅_0$ est la valeur de la résistance pour $𝑃 = 𝑃_{atm}$.
Le matériau piézorésistif est placé dans le circuit représenté sur la figure 3 ci- dessous.
$𝐸$ est une tension continue constante. $𝑅_1$ est une résistance variable. $𝑅_3$ et $𝑅_4$ (ici il y a une erreur dans l’énoncé, on parle de $R_3$ et $R_2$) sont des résistances constantes. $𝑢_{mes}$ est la tension mesurée.
6. On cherche à exprimer $𝑢_{mes}$ en fonction des données de l’énoncé.
a. Exprimer $𝑢_1$ en fonction de $𝑅_1, 𝑅_2 et 𝐸$, puis $𝑢_3$ en fonction de $𝑅_3, 𝑅 et 𝐸$.
Pour $u_1$ en fonction de $R_1, R_2 et E$ :
On applique la loi des mailles dans la maille du circuit contenant les tensions $u_1, u_2 et E$ dans le sens horaire, on obtient :
$u_1 + u_2 – E = 0$ , soit $u_1 = E – u_2$ $=E – R_2 i$ avec i le courant traversant la branche contenant les résistances $R_1$ et $R_2$.
On a alors $i = \frac{u_2}{R_2} = \frac{u_1}{R_1}$
$\Rightarrow$ $u_1 = E – \frac{R_2 u_1}{R_1}$ $\Rightarrow$ $u_1[1 + \frac{R_2}{R_1}] = E$ $\Rightarrow$ $u_1 = \frac{E}{\frac{R_1 + R_2}{R_1}}$ $= \frac{E R_1}{R_1 + R_2}$
Pour $u_3$ en fonction de $R_3, R et E$ :
On applique la loi des mailles dans la maille du circuit contenant les tensions $u_3, u et E$ dans le sens horaire, on obtient :
$u_3 + u – E = 0$ , soit $u_3 = E – u$ $=E – R i’$ avec i’ le courant traversant la branche contenant les résistances $R_3$ et $R$.
On a alors $i’ = \frac{u}{R} = \frac{u_3}{R_3}$
$\Rightarrow$ $u_3 = E – \frac{R u_3}{R_3}$ $\Rightarrow$ $u_3[1 + \frac{R}{R_3}] = E$ $\Rightarrow$ $u_3 = \frac{E}{\frac{R_3 + R}{R_3}}$ $= \frac{E R_3}{R_3 + R}$
b. En déduire que $𝑢_{mes} = (\frac{R_1}{R_1 + R_2} - \frac{R_3}{R + R_3})E$
Dans la maille en haut à gauche du circuit, en appliquant la loi des mailles dans le sens horaire on obtient :
$u_1 – u_{mes} – u_3 = 0$ , $\Rightarrow$ $u_{mes} = u_1 – u_3 $ $= \frac{R_1 E}{R_1 + R_2} – \frac{R_3 E}{R + R_3}$ $= (\frac{R_1}{R_1 + R_2} – \frac{R_3}{R + R_3})E$
7. On veut ajuster la résistance $𝑅_1$ afin d’avoir $𝑢_{mes} = 0$ lorsque $𝑃 = 𝑃_{atm}$. Déterminer l’expression de $𝑅_1$ permettant d’avoir $𝑢_{mes} = 0$ lorsque $𝑃 = 𝑃_{atm}$, en fonction de $𝑅_0, 𝑅_2 et 𝑅_3$.
On recherche la valeur de $R_1$ lorsque $R=R_0$ et $u_{mes}=0$.
$\Rightarrow$ $\frac{R_1}{R_1+R_2} = \frac{R_3}{R_0+R_3}$ $\Rightarrow$ $R_1 R_0 + R_1 R_3 = R_1 R_3 + R_2 R_3$ $\Rightarrow$ $R_1 [R_0 + R_3 – R_3] = R_2 R_3$ $\Rightarrow$ $R_1 = \frac{R_2 R_3}{R_0}$
8. On considère une variation de pression $Δ𝑃$ positive par rapport à $𝑃_{atm}$ de sorte que : $𝑃 = 𝑃_{atm} + Δ𝑃$.
a. Montrer que la résistance $𝑅$ peut s’écrire sous la forme $𝑅 = 𝑅_0 + Δ𝑅$. Exprimer $Δ𝑅$ en fonction de $𝑘, Δ𝑃 et 𝑅_0$.
On sait que : $R=R_0[1 + k(P – P_{atm})]$, avec ici, $P = P_{atm} + \Delta P$ on obtient :
$R=R_0[1 + k( P_{atm} + \Delta P – P_{atm})]$ $=R_0[1 + k \Delta P]$ $=R_0 + k R_0 \Delta P$
On retrouve un $\Delta R = k R_0 \Delta P$
b. En pratique, pour les pressions artérielles usuelles, le coefficient de piézorésistivité $𝑘$ et la variation de pression $Δ𝑃$ sont tels que $Δ𝑅 ≪ 𝑅_0$ ($Δ𝑅$ très petit devant $𝑅_0$). Proposer une condition reliant $𝑘$ et $Δ𝑃$ pour avoir $Δ𝑅 ≪ 𝑅_0$. Cette condition est supposée remplie dans la suite.
Si $Δ𝑅 ≪ 𝑅_0$ alors $k R_0 ΔP ≪ 𝑅_0$ $\Rightarrow$ $k ΔP ≪ 1$ soit $ ΔP ≪ \frac{1}{k}$
c. Montrer qu’à une variation de pression $Δ𝑃$ est associée une tension mesurée $𝑢_{mes} ≃ \frac{𝑅_3}{(𝑅_0 + 𝑅_3)^2} \times 𝑅_0 × 𝑘 Δ𝑃 × 𝐸$ En déduire l’expression de la sensibilité du transducteur de pression $𝑆 = \frac{𝑢_{mes}}{Δ𝑃}$ en fonction des données de l’énoncé. Précisé l’unité de $𝑆$ et donner le sens physique de cette grandeur.
Nous avons :
$𝑢_{mes} = (\frac{R_1}{R_1 + R_2} – \frac{R_3}{R + R_3})E$ $\Rightarrow$ $𝑢_{mes} = (\frac{R_1}{R_1 + R_2} – \frac{R_3}{R_0 + \Delta R + R_3})E$ $\Rightarrow$ $𝑢_{mes} = (\frac{R_1}{R_1 + R_2} – \frac{R_3}{R_0 + k R_0 \Delta P + R_3})E$ $\Rightarrow$$𝑢_{mes} = (\frac{R_1 R_0 + k R_1 R_0 \Delta P + R_1 R_3 – R_3 R_1 – R_2 R_3}{(R_1 + R_2)(R_0 + k R_0 \Delta P + R_3)})E$ $\Rightarrow$ $𝑢_{mes} = (\frac{R_1 R_0 + k R_1 R_0 \Delta P – R_2 R_3}{(R_1 + R_2)(R_0 + k R_0 \Delta P + R_3)})E$ ,
Or $R_1 R_0 = R_2 R_3$ et $R_1 + R_2 = \frac{R_2 R_3}{R_0} + R_2$ $=\frac{R_2}{R_0}(R_3 + R_0)$, on a alors :
$𝑢_{mes} = (\frac{k R_1 R_0 \Delta P }{\frac{R_2}{R_0}(R_3 + R_0)(R_0 + k R_0 \Delta P + R_3)})E$ $\Rightarrow$ $𝑢_{mes} = (\frac{k R_3 R_0 \Delta P }{(R_3 + R_0)(R_0 + k R_0 \Delta P + R_3)})E$ $\Rightarrow$ $𝑢_{mes} = (\frac{k R_3 R_0 \Delta P }{(R_3 + R_0)^2})E$ car $\Delta R << R_0$
Unité de S : $\frac{[Volt]}{[Pascal]}$ représente la variation de la tension mesurée pour une variation de pression du matériau.
9. Expliquer en quelques lignes comment ce système peut être utilisé pour mesurer les variations de pression artérielle $Δ𝑃$ en fonction du temps.
Le matériau peut être placé au sein du milieu dont la pression est étudiée. Lors d’un changement de pression, une variation de la tension pourra être lue directement, cette tension est liée à l’intensité de la variation de la pression et varie instantanément.
C. Exploitation des mesures de pression artérielle systémique.
Dans toute cette sous-partie C, toutes les valeurs de pression artérielle correspondent à la pression
différentielle $Δ𝑃 = 𝑃 − 𝑃_{atm}$. Par exemple, une pression artérielle de $120 mmHg$ correspond à une pression absolue de $760 mmHg + 120 mmHg = 840 mmHg$. De plus, toutes les mesures sont prises pour un individu allongé et au repos.
10. Une mesure de pression artérielle en fonction du temps est donnée ci-après figure 5.
a. Déterminer la pression artérielle systolique $Δ𝑃_{a,sys}$, la pression artérielle diastolique $Δ𝑃_{a,dia}$ et estimer la pression artérielle moyenne $Δ𝑃_{a,moy}
$Δ𝑃_{a,sys} = 129 mmHg$
$Δ𝑃_{a,dia} = 80 mmHg$
$Δ𝑃_{a,moy} = 104.5 mmHg$
b. Les médecins utilisent fréquemment la formule $𝑃_{a,moy} = \frac{Δ𝑃_{a,sys} + 2Δ_{𝑃a,dia}}{3}$ pour calculer la pression artérielle moyenne.
Après avoir vérifié la cohérence de cette formule avec la question précédente, justifier qualitativement la différence de pondération entre la pression systolique et diastolique.
Par ce calcul on obtient : $𝑃_{a,moy} = 96,3 mmHg$ ce qui est proche de celle trouvée dans la question précédente.
Pour expliquer le fait que l’on prend en compte dans la moyenne 2 fois plus la valeur de la pression diastolique par rapport à celle systolique il fait observer que sur le graphe la pression systolique apparait sur un temps très court.
c. Estimer la fréquence cardiaque 𝑓 en battements par minute (notés battements.$min^{−1}$).
Sur le graphe on trouve une période T=1s soit une fréquence f=1Hz=1battement/seconde ce qui équivaut à $60 battements.min^{-1}$
d. Sachant que le débit de volume de sang est de $𝐷_𝑉 = 5,0 L.min^{−1}$ au repos, déterminer le volume de sang $𝑉_1$ envoyé par le cœur à chaque battement. On exprimera $𝑉_1$ en mL.
Le coeur envoie 5L par minute et il bat 60 fois pendant ce délai. Pour chaque battement il envoie : $V_1 = \frac{5}{60}=83,3mL$
e. Le spectre de la pression artérielle contient-il des harmoniques ? Justifier.
Lorsqu’un motif se répète de façon périodique alors il y a une ou plusieurs harmoniques dans le spectre en fréquence. Ici les pulsations se répètent toute les secondes, il y aura alors une harmonique correspondant à la fréquence 1Hz.
f. Quel type de filtrage est adapté pour déterminer la pression artérielle moyenne ? On précisera la fréquence de coupure du filtre.
Sur le graphe il faudrait appliquer un filtre qui supprime les pics représentant les battements cardiaques. Or on a une fréquence de 1Hz (q.10c) . Il faut alors supprimer les basses fréquences en utilisant un filtre passe-haut de fréquence de coupure supérieure à 1Hz
II. Introduction à l’hémodynamique
L’hémodynamique (ou « dynamique du sang ») est la science des propriétés physiques de la circulation sanguine en mouvement dans le système cardiovasculaire.
On propose dans cette partie d’étudier de manière simplifiée quelques aspects de l’hémodynamique.
Dans toute cette partie II l’individu est allongé et au repos.
A. Écoulement dans un vaisseau sanguin
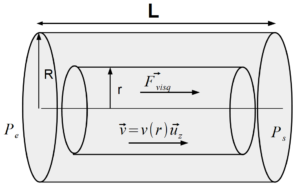
On s’intéresse d’abord à l’écoulement horizontal du sang dans un seul vaisseau sanguin qu’on assimile à une conduite cylindrique indéformable de diamètre $𝑑$ et de longueur $𝐿$ (voir figure 6 ci-dessous).
Le sang est un fluide incompressible de masse volumique $𝜌_s = 1 060 kg.m^{−3}$. De plus, dans un souci de simplicité, on considérera que le sang est un fluide newtonien de viscosité dynamique égale à $𝜂_s = 1,6 × 10^{−3} Pa.s $.
L’écoulement du sang est supposé stationnaire et laminaire.
Le gradient de pression est uniforme le long de la conduite et on note $Δ𝑃 = 𝑃(𝑥 = 0) − 𝑃(𝑥 = 𝐿) > 0$ la différence de pression entre le début et la fin du vaisseau sanguin considéré.
Le champ des vitesses est de la forme $\vec{𝑣} = 𝑣(𝑟) \vec{u_x}$ en coordonnées cylindriques d’axe $(𝑂𝑥)$.
Enfin, la force de viscosité que le sang à l’extérieur du cylindre de rayon $𝑟 ≤ \frac{𝑑}{2}$, d’axe $(𝑂𝑥)$ et de longueur $𝐿$ exerce sur le sang situé à l’intérieur de ce cylindre s’écrit : $\vec{𝐹_{visc}} = 2𝜋𝑟𝐿𝜂_s \frac{d𝑣(𝑟)}{d𝑟} \vec{𝑢_𝑥}$ .
11. À partir d’un bilan de quantité de mouvement sur un système à expliciter, montrer que la vitesse du fluide s’exprime selon : $\vec{𝑣} = \frac{Δ𝑃}{4𝜂_s 𝐿} (\frac{𝑑^2}{4} − 𝑟^2) \vec{𝑢_𝑥}$ .
Cette démonstration fait partie des démonstrations à savoir refaire comme indiqué dans le Bulletin Officiel (BO).
On étudie l’écoulement unidimensionnel d’un fluide visqueux dans un cylindre horizontal de rayon R et de longueur L, en régime stationnaire (indépendant du temps). On suppose un écoulement laminaire (Re<2000). on néglige la pesanteur.
On considère une portion dufluide cylindrique, de rayon r et de longueur L.
Il existe une pression en entrée différente de la pression en sortie ce qui permet le déplacement du fluide.
En régime stationnaire, la variation de quantité de mouvement est nulle, soit : $\sum \vec{F} = \frac{d \vec p}{dt} = 0$
Les forces qui s’appliquent sur le volume de fluide sont les forces pressentes en entrée et en sortie ainsi que la force visqueuse due au sang à l’extérieur. Le poids est négligé.
$\vec{F_{pe}} – \vec{F_{ps}} + \vec {F_{visq}} = 0$
$P_{e} S \vec{u_x} – P_{s} S \vec{u_x} + 2 \pi r L \eta_S \frac{d v(r)}{dr} \vec {u_x} = 0$
$P_{e} \pi r^2 – P_{s} \pi r^2 + 2 \pi r L \eta_S \frac{d v(r)}{dr} = 0$
Soit : $\frac{dv(r)}{dr}= – \frac{\Delta P r}{2 L \eta_S}$
On intègre alors entre un rayon r et le rayon R (ici on choisi les bornes d’intégration entre r et R car la vitesse en R est nulle v(r=R)=0 et la borne r nous permettra d’avoir la vitesse v(r))
$\int _{v(r)}^{v(r=R)}\frac{dv(r)}{dr}= – \int _r^R \frac{\Delta P r}{2 L \eta_S}$
$[v]_{v(r)}^{v(r=R)} = – \frac{\Delta P }{2 L \eta_S} [\frac{r^2}{2}]_r^R$
$0-v(r) = – \frac{\Delta P }{2 L \eta_S} [\frac{R^2 – r^2}{2}]$
Soit : $v(r) = \frac{\Delta P }{4 L \eta_S} [\frac{d^2}{4} – r^2]$
Représenter ensuite le champ des vitesses dans une section droite de conduite.
12. En déduire l’expression du débit de volume $𝐷_𝑉$ en fonction des données de l’énoncé
Le débit volumique $D_V = \iint _S v dS$ $=\iint _S \frac{\Delta P}{4 \eta _S L}(\frac{d^2}{4} – r^2)dS$
Or $dS = rd \theta dr$ et $\frac{d^2}{4} = R^2$
On a alors : $D_V=\int _0^{2\pi} d\theta \int_0^R \frac{\Delta P}{4 \eta _S L}(R^2 – r^2)rdr$ $=2\pi \frac{\Delta P}{4 \eta _S L } \int_0^R (R^2 – r^2)rdr$ $=\pi \frac{\Delta P}{2 \eta _S L } \int_0^R (R^2 r – r^3)dr$ $=\pi \frac{\Delta P}{2 \eta _S L } [(\frac{R^2 r^2}{2} – \frac{r^4}{4})]_0^R $ $=\pi \frac{\Delta P}{2 \eta _S L } [(\frac{R^4 }{2} – \frac{R^4}{4})]$ $=\pi \frac{\Delta P R^4}{8 \eta _S L }$
13. On définit la résistance hydraulique de sorte que $Δ𝑃 = 𝑅_h 𝐷_𝑉$. Montrer que la résistance hydraulique s’exprime sous la forme : $𝑅_h = \frac{128𝜂_s𝐿}{𝜋𝑑^4}$ .
$Δ𝑃 = 𝑅_h 𝐷_𝑉$ donc : $R_h = \frac{\Delta P}{𝐷_𝑉}$ $=\frac{\Delta P 8 \eta _S L}{\Delta P \pi R^4}$ $=\frac{8 \eta _S L}{\pi R^4}$ $=\frac{128 \eta _S L}{\pi d^4}$
Dans la suite du sujet, la relation $Δ𝑃 = 𝑅_h 𝐷_𝑉$ avec $𝑅_h = \frac{128𝜂_s 𝐿}{𝜋𝑑^4}$ constitue la loi de Poiseuille.
B. Prise en compte de l’ensemble des vaisseaux sanguins.
On souhaite prendre en compte l’ensemble des vaisseaux sanguins de la circulation systémique pour estimer la perte de charge entre la sortie du cœur gauche et l’entrée du cœur droit.
On se propose de calculer la perte de charge due aux artérioles afin d’effectuer une comparaison avec les données réelles. On supposera que la loi de Poiseuille peut s’appliquer dans tous les vaisseaux sanguins.
14. À partir du tableau 1, déterminer le débit de volume du sang dans l’aorte $𝐷_𝑉$.
Justifier ensuite que le nombre d’artérioles dans le corps humain vaut environ $𝑁_{artérioles} ≃ 1,5 × 10^6$.
Le piège ici est de partir de la formule du débit volumique trouvée question 12 en prenant la pression dans l’aorte comme étant $\Delta P$. Or $\Delta P$ représente la variation de pression entre l’entrée et la sortie de l’aorte (information que l’on a pas!)
On doit repartir de la formule du débit volumique liant vitesse et section : $D_V = vS$ $=\frac{v \pi d^2}{4}$
AN : $D_V = \frac{2,65.10^{-1} \pi (20.10^{-3})^2}{4} = 8,32.10^{-5} m^3 . s^{-1}$ , soit $D_V=8,32cL.s^{-1}$
Pour trouver le nombre d’artérioles, il faut garder en tête que le débit volumique est conservatif, de plus les artérioles sont mis en dérivation donc $D_{V,aorte}= N_{artérioles} \times D_{V,artérioles}$
On retrouve le débit volumique d’une artériole en utilisant la formule définie à la question précédente :
$D_{V,artérioles}=\frac{v \pi d^2}{4} $
AN :
$D_{V,artérioles}=\frac{2,80.10^{-2} \pi (0,05.10^{-3})^2}{4}=5,5.10^{-11} m^3 .s^{-1} $
Au final :
$ N_{artérioles} = \frac{D_{V,aorte}}{D_{V,artérioles}}$
AN :
$ N_{artérioles} = \frac{8,32.10^{-5}}{5,5.10^{-11}} \simeq 1,5.10^6$
15. En prenant $𝐷_𝑉 = 5,0 L.min^{−1}$, estimer les pertes de charge $Δ𝑃_{artérioles}$ dans les artérioles. Comparer cette valeur à celle pouvant être déterminée à partir du tableau 1. Commenter et proposer une brève explication aux écarts observés entre les deux valeurs.
$\Delta P = R_h D_V = \frac{128 \eta _S L}{\pi d^4} D_V$
AN :
$\Delta P = \frac{128 1,6.10^{-3}.10.10^{-3}}{\pi (0,05.10^{-3})^4} \frac{5.10^{-3}}{60} = 5794Pa$
D’après le tableau 1. La pression en entrée d’artériole est de 86 mmHg et en sortie 30mmHG (équivalent à la pression en entrée de capillaires) soit une différence de 56mmHg équivalent à une différence de pression de 7464Pa
La différence peut provenir de l’approximation faite sur le débit volumique.
C. Aspects énergétiques
À partir des mesures de pression moyenne du tableau 1, on cherche à estimer la puissance moyenne consommée au repos par le cœur pour pomper le sang.
Pour simplifier, on considérera que le cœur agit comme une pompe qui fonctionne en continu. Cela revient à considérer uniquement les valeurs de pression moyenne
16. Justifier précisément que la puissance du cœur gauche $𝒫_g$ nécessaire pour faire remonter la pression sanguine de 5 à $100 mmHg$ s’exprime par $𝒫_g = 𝐷_𝑉 × Δ𝑃_g$ où $Δ𝑃_g = 100 mmHg − 5 mmHg$ est la différence de pression entre le ventricule gauche et l’atrium gauche.
Faire ensuite l’application numérique pour $𝐷_𝑉 = 5,0 L.min^{−1}$ et exprimer la puissance en watt.
De même, déterminer la valeur numérique de la puissance du cœur droit $𝑃_d$ nécessaire pour faire
remonter la pression sanguine de 3 à $25 mmHg$.
On peut partir du bilan énergétique entre le ventricule gauche et l’atrium :
$\delta m \Delta(\frac{1}{2} v^2 + gz + \frac{P}{\rho}) = W_g + W_d$
avec $W_d=0$ car on ne considère pas les pertes et $W_g$ représentant le travail utile du coeur.
Si on divise par $\delta t$ , on obtient :
$D_m \Delta(\frac{1}{2} v^2 + gz + \frac{P}{\rho}) = P_g $
Or, on peut considérer la variation d’altitude comme négligeable ainsi que la variation de vitesse.
$D_m \Delta( \frac{P}{\rho}) = P_g $
$\rho D_V \Delta( \frac{P}{\rho}) = P_g $
$D_V \Delta( {P}) = D_V (P_{ventricule} – P_{atrium}) = D_V \Delta P_g = P_g $
Calcul de la puissance en Watt :
$P_g = \frac{5.10^{-3}}{60} \times \frac{(100-5) \times 1,013.10^5}{760} = 1,05W$
De la même façon, $P_d = \frac{5.10^{-3}}{60} \times \frac{(25-3) \times 1,013.10^5}{760} = 0,24W$
17. Expliquer pourquoi le cœur gauche est plus développé que le cœur droit.
Le cœur gauche doit maintenir une différence de pression plus important que le cœur droit. On le voit clairement sur la puissance nécessaire. C’est pour cela qu’il est plus développé.
18. Montrer que le travail fourni par le cœur au sang en un jour vaut $𝑊_{coeur} ≃ 112 kJ$
On calcule d’abord la puissance totale du coeur soit $P= P_g + P_d = 1,294W$ que l’on applique sur le temps d’une journée :
$W_{coeur} = P \times t$
Application Numérique:
$W_{coeur} = 1,294 \times 3600 \times 24= 111,8kJ$
19. Le rendement énergétique du muscle cardiaque étant de $20 %$, déterminer l’énergie consommée par
jour par l’individu au repos pour pomper le sang.
Exprimer le résultat en joule puis en kilocalorie kcal.
Comparer cette énergie aux besoins énergétiques journaliers qui est de l’ordre de $2 × 10^3 kcal$ pour un
homme. Commenter.
Donnée : 1 kcal = 4,18 kJ
Formule du rendement : $\frac{W_u}{W_a} = \eta$
avec $W_u=W_{coeur}$
Soit :
$W_a = \frac{W_u}{\eta}$
Application Numérique :
$W_a= \frac{112}{\frac{20}{100}} = 560kJ = 134kcal$
Ce qui représente approximativement 6,7% des besoins journaliers.
III. L’oxygénation du sang dans les capillaires pulmonaires.
Le bon fonctionnement des organes nécessite un apport en dioxygène régulier. Dans cette partie on propose d’étudier l’oxygénation du sang dans les capillaires pulmonaires.
On aborde l’oxygénation du sang par une approche de diffusion de particules. Dans un souci de simplification, plusieurs processus ne sont pas pris en compte comme la capture du dioxygène par les globules rouges ou bien le transport de dioxygène par convection dans les capillaires pulmonaires.
A. Modèle unidimensionnel en régime stationnaire.
On se propose d’établir l’équation de la diffusion concernant la concentration en dioxygène $O_2$ dans un capillaire pulmonaire. On néglige le transport du dioxygène par convection dans les capillaires sanguins.
On s’intéresse à un capillaire pulmonaire assimilable à un tube cylindrique (de rayon $𝑎$ et de longueur $𝐿$) d’axe $𝑥$ caractérisé par une concentration en dioxygène $𝐶_{O_2}(𝑥)$ (voir schéma figure 9 ci-contre). La concentration en dioxygène est supposée uniforme sur toute section du cylindre orthogonale à $𝑂𝑥$.
On considère le régime stationnaire. On note $𝐶_{O_2}(𝑥 = 0) = 𝐶_1$ la concentration molaire en $O_2$ à l’entrée du capillaire et $𝐶_{O_2}(𝑥 = 𝐿) = 𝐶_2$ la concentration molaire à la sortie du capillaire. On note $Φ(𝑥)$ le flux algébrique de $O_2$ rentrant en $𝑥$ dans le sens de $\vec{𝑢_𝑥}$.
Pour tenir compte de l’apport de molécules de $O_2$ par diffusion à travers la membrane alvéolo-capillaire on considère un flux latéral de particules.
Le flux latéral de particules entrant par une surface latérale de cylindre $d𝑆_{lat} = 𝜋𝑎d𝑥$ s’exprime par $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ où $𝐶_{ext}$ est la concentration en dioxygène dans l’alvéole pulmonaire et $ℎ$ est la perméabilité de la membrane alvéolo-capillaire. Cet apport latéral se fait sur la moitié supérieure de la surface latérale du cylindre.
$𝐶_{ext}$ est supposée constante. Le capillaire est suffisamment long pour considérer que $𝐶_{ext} = 𝐶_2 > 𝐶_1$.
On choisit d’exprimer toutes les concentrations en $mol.m^{−3}$ et tous les flux en $mol.s^{−1}$.
20.Préciser l’unité de $ℎ$ en fonction des unités de base du système international.
$dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ soit : $h = \frac{d \Phi_{lat}}{[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}}$ $=\frac{[mol].[s]^{-1}}{[mol].[m]^{-3}.[m]^2}$ $=\frac{[m]}{[s]}$
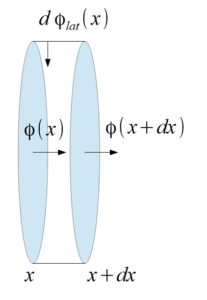
21.En faisant un bilan de particules sur une tranche de cylindre comprise entre $𝑥$ et $𝑥 + d𝑥$, montrer que le flux $Φ(𝑥)$ suit l’équation différentielle suivante : $\frac{dΦ}{d𝑥} = 𝜋𝑎ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]$
Nous travaillons sur un élément de volume représenté ci-dessous :
En faisant un bilan particulaire des flux et en prenant $\Phi(x)$ comme étant le flux entrant et $\Phi(x+dx)$ le flux sortant, on obtient :
$\Phi(x) – \Phi(x+dx) + d\Phi_{lat} =0$ $\Rightarrow$ $- \frac{d \Phi(x)}{dx}dx + h [C_{ext} – C_{O_2} (x)]dS_{lat} =0$ $\Rightarrow$ $-\frac{d\Phi(x)}{dx} dx + h [C_{ext} – C_{O_2} (x)]\pi a dx = 0$ $\Rightarrow$ $\frac{d\Phi(x)}{dx}= \pi a h [C_{ext} – C_{O_2} (x)]$
22.Rappeler la loi de Fick. En déduire une relation entre $Φ(𝑥)$ et $𝐶_{O_2}(𝑥)$. On notera $𝐷_{O_2}$ le coefficient de diffusion du dioxygène dans le sang et on exprimera l’unité de $𝐷_{O_2}$ en fonction des unités de base du système international.
Loi de Fick : $\Phi(x)= – D_{O_2} \times S \times \frac{dC}{dx}$, ce qui donne par dérivation :
$\frac{d \Phi(x)}{dx} = – D_{O_2} \times S \times \frac{d^2C}{dx^2}$
Unité de $ D_{O_2}$ :
$ D_{O_2} = \frac{\Phi \times dx}{dC \times S} =\frac{[mol].[s]^{-1} .[m]}{[mol].[m]^{-3} [m]^2} $$=\frac{[m]^2}{[s]}$
23.En déduire que l’équation différentielle vérifiée par $𝐶_{O_2}(𝑥)$ peut se mettre sous la forme suivante :
$\frac{d^2 𝐶_{O_2}}{d𝑥^2} − \frac{𝐶_{O_2}(𝑥) − 𝐶_{ext}}{ℓ^2} = 0$ avec $ℓ^2 = \frac{𝐷_{O_2}𝑎}{ℎ}$
Faire l’application numérique pour $ℓ$ et donner un sens physique à ce paramètre.
Données :
▷ Rayon typique d’un capillaire pulmonaire : $𝑎 = 4,0 μm$
▷ Perméabilité de la membrane alvéolo-capillaire : $ℎ = 66 × 10^{−6} unités SI$
▷ Coefficient de diffusion de $O_2$ dans le sang : $𝐷_{O_2} = 1,7 × 10^{−7} unités SI$
$\frac{d \Phi(x)}{dx} = – D_{O_2} \times S \times \frac{d^2C}{dx^2}$
Or, $\frac{d \Phi(x)}{dx} =\pi a h [C_{ext} – CO_2 (x)]$ $\Rightarrow$ $- D_{O_2} \times S \times \frac{d^2C}{dx^2} = \pi a h [C_{ext} – CO_2 (x)]$ $\Rightarrow$ $D_{O_2} S \frac{d^2C}{dx^2} + \pi a h [C_{ext} – CO_2 (x)]=0$ $\Rightarrow$ $\frac{d^2C}{dx^2} + \frac{\pi a h}{D_{O_2} S}[C_{ext} – CO_2 (x)] = 0$
$S = \pi a^2$ $\Rightarrow$ $\frac{d^2C}{dx^2} + \frac{[C_{ext} – CO_2 (x)]}{l^2} = 0$, avec $l^2 = \frac{D_{O_2} a}{h}$
Application Numérique :
$l = \sqrt{\frac{1,7.10^{-7} \times 4.10^{-6}}{66.10^{-6}}}= 5,1.10^{-5}m$ avec l homogène à une distance et représentant la distance de diffusion pour le régime permanent.
24.La solution de l’équation différentielle de la question 23. peut s’écrire sous la forme suivante :
$𝐶_{O_2}(𝑥) = 𝐴 + 𝐵e^{−𝑥/ℓ} + 𝐶e^{𝑥/ℓ}$
a.La longueur d’un capillaire pulmonaire $𝐿$ est typiquement de 1 mm. En comparant $ℓ$ et $𝐿$, expliquer succinctement que l’on puisse considérer que $𝐿 = +∞$ dans la suite.
$l \simeq 10^{-5}$ et $L \simeq 10^{-3}$, donc $l<<L$, on peut alors considérer que $L = + \infty$
b.Déterminer les constantes $𝐴$, $𝐵$ et $𝐶$ en fonction des données de l’énoncé
Les conditions limites sont : $C_{O_2} (x=0) = C_1$ et $C_{O_2} (x=L) = C_2$
$C_{O_2} (x=0) = A+B+C = C_1$
$C_{O_2} (x=L) =A+ Be^{-\infty} + Ce^{+\infty} = C_2$ ce qui implique $C = 0$(pour ne pas que la solution diverge) et $A=C_2$
Or, $A+B+C = C_1$ $\Rightarrow$ $B=C_1 – C_2$
Au final :
$C_{O_2}(x)= C_2 + (C_1 – C_2)e^{- \frac{x}{l}}$
c.Tracer l’allure de $𝐶_{O_2}(𝑥)$ et faire apparaître $ℓ$ sur votre graphique.
25. Montrer que la quantité de dioxygène transférée par unité de temps de l’alvéole pulmonaire vers le capillaire pulmonaire s’exprime, en moles par seconde, par la relation : $Φ_{lat,1 capillaire} = ℎ (𝐶_{ext} − 𝐶_1) × 𝜋𝑎$
Le flux latéral s’exprime par : $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]d𝑆_{lat}$ $\Rightarrow$ $dΦ_{lat} = ℎ[𝐶_{ext} − 𝐶_{O_2}(𝑥)]\pi a dx$ , nous connaissons maintenant l’expression de $C_{O_2}(x)$
$\Rightarrow$ $dΦ_{lat} = ℎ[𝐶_{ext} −(C_2-(C_1 – C_2)e^{- \frac{x}{l}})]\pi a dx$, de plus $C_2 = C_{ext} $
$\Rightarrow$ $dΦ_{lat} = ℎ[(C_2 – C_1)e^{- \frac{x}{l}})]\pi a dx$
$\Rightarrow$ $\int dΦ_{lat} = \int_0^L ℎ[(C_2 – C_1)e^{- \frac{x}{l}})]\pi a dx$
$\Rightarrow$ $Φ_{lat,1 capillaire} = \int_0^L ℎ \pi a ((C_2 – C_1)e^{- \frac{x}{l}})) dx$
$\Rightarrow$ $Φ_{lat,1 capillaire} = ℎ \pi a [((C_2 – C_1)\times ( -l e^{- \frac{x}{l}})))]_0^L$
$\Rightarrow$ $Φ_{lat,1 capillaire} =-l ℎ \pi a (C_2 – C_1) ( e^{- \frac{L}{l}} – e^{- \frac{0}{l}} )))]$
$\Rightarrow$ $Φ_{lat,1 capillaire} =-l ℎ \pi a (C_2 – C_1) ( – 1 )))]$
$\Rightarrow$ $Φ_{lat,1 capillaire} =l ℎ \pi a (C_{ext} – C_1)))]$
B. Estimation de la consommation d’oxygène
En pratique, les données d’oxygénation du sang dans les capillaires pulmonaires ne sont pas données en terme de concentration en $mol.m^{−3}$ mais en terme de pression partielle de dioxygène $𝑃_{O_2}$ en mmHg.
Afin de pouvoir comparer des données réelles aux résultats de la partie précédente, nous avons besoin d’introduire le coefficient de Henry $𝜎$ tel que $𝐶_{O_2} = 𝜎 × 𝑃_{O_2}$
Pour le dioxygène dans le sang, on prendra $𝜎 = 1,7 × 10^{−3} mol.m^{−3}.mmHg^{−1}$
Ainsi, la quantité de dioxygène transférée par unité de temps (en $mol·s^{−1}$) de l’alvéole pulmonaire vers le capillaire pulmonaire (voir question 25.) s’exprime en fonction des pressions partielles sous la forme suivante :
$Φ_{lat,1 capillaire} = ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
avec $𝑃_{O_2,ext}$ la pression partielle en dioxygène dans une alvéole pulmonaire et $𝑃_{O2,1}$ la pression partielle en dioxygène à l’entrée d’un capillaire pulmonaire.
En prenant en compte qu’il y a $𝑁$ capillaires pulmonaires placés en parallèle qui permettent l’oxygénation du sang, la quantité de dioxygène transférée par unité de temps (en $mol·s^{−1}$) vers tous les capillaires pulmonaires s’exprime par :
$Φ_{lat,𝑁 capillaires} = 𝑁 × Φ_{lat,1 capillaire} = 𝑁 × ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
26. Déterminer le volume molaire $𝑉_𝑚$ d’un gaz parfait à $25 °C$ sous pression atmosphérique $𝑃_{atm} = 1,013 bar$.
Donnée : Constante des gaz parfaits : $𝑅 = 8,314 J.mol^{−1}.K^{−1}$
$V_m = \frac{V}{N} = \frac{RT}{P}$
Application Numérique :
$V_m = \frac{8,314 \times (25+273)}{1,013.10^5} = 2,44.10^{-2} m^3 .mol^{-1}$
On souhaite estimer le volume de dioxygène transféré par minute des alvéoles-pulmonaires vers les capillaires sanguins en utilisant le modèle développé dans cette partie III.
Pour un individu adulte au repos, le nombre de capillaires pulmonaires fonctionnels est de $𝑁 ≃ 20 × 10^9$ et les pressions partielles en dioxygène sont $𝑃_{O_2,ext} = 100 mmHg$ et $𝑃_{O_2,1} = 40 mmHg$.
27.Déterminer le volume de dioxygène transféré par minute des poumons vers les capillaires pulmonaires. On notera $𝑉_{O_2}$ cette quantité et on l’exprimera en $L.min^{−1}$.
Données :
▷ Rayon typique d’un capillaire pulmonaire : $𝑎 = 4,0 μm$
▷ Perméabilité de la membrane alvéolo-capillaire : $ℎ = 66 × 10^{−6} unités SI$
▷ Coefficient de Henry : $𝜎 = 1,7 × 10^{−3} mol.m^{−3}.mmHg^{−1}$
Pour connaitre le volume de dioxygène transféré il faut repartir de la formule du flux qui nous donne le flux de dioxygène en $mol.s^{-1}$ :
$Φ_{lat,𝑁 capillaires} = 𝑁 × ℎ𝜎 × (𝑃_{O_2,ext} − 𝑃_{O2,1}) × 𝜋𝑎ℓ$
Nous connaissons toute les valeurs, nous pouvons passer à l’application numérique (on peut garder les valeurs de pression en mmHG car le coefficient de Henry est en $mmHg^{-1}$) :
Application Numérique :
$Φ_{lat,𝑁 capillaires} = 20.10^9 \times 66.10^{-6} \times 1,7.10^{-3} \times (100-40) \times \pi \times4.10^{-6} \times 5,1.10^{-5}$ $=8,63.10^{-5} mol.s^{-1}$ , or $V_m=2,4.10^{-2}m^3 . mol^{-1}$, donc :
$Φ_{lat,𝑁 capillaires} = 8,63.10^{-5}\times 2,4.10^{-2}$ $=2,07.10^{-6} m^3 .s^{-1} = 2,07.10^{-3} L.s^{-1}$ $ = 0.12L.min^{-1}$
28.Comparer votre valeur de consommation d’oxygène à la valeur typiquement mesurée pour un individu adulte en bonne santé au repos : $𝑉_{O_2} ≃ 0,2 L.min^{−1}$.
Les valeurs sont du même ordre de grandeur, la différence peut provenir de la valeur de volume molaire prise pour le calcul, en effet, la pression et la température n’est pas égale à celles prises pour le calcul du volume molaire.