Physique BCPST
A BCPST | 2023
Sujet physique A BCPST 2023
Ce sujet est composé de 3 parties indépendantes. La première partie modélise un phénomène optique atmosphérique connu sous le nom de « halo solaire ». La seconde partie aborde l’étude de la fonte de la glace des inlandsis de l’Antarctique et du Groënland. La troisième et dernière partie concerne quelques propriétés hydrodynamiques des glaciers. Un ensemble de données numériques utiles est disponible au début du sujet. En Annexe A, en fin de sujet, sont explicitées quelques fonctions du langage Python.
Certaines questions, repérées par une barre en marge, ne sont pas guidées et demandent une prise d’initiative de la part du candidat. Les pistes de recherche doivent être consignées par le candidat sur sa copie. L’évaluation des réponses à ces questions tient autant compte de la démarche entreprise que des résultats obtenus.
Toutes les réponses doivent être dûment justifiées
Données numériques utiles
Célérité de la lumière dans le vide $𝑐 = 3,0 × 10^8 m.s^{−1}$
Indice optique de l’air $𝑛_𝑎 = 1,00$
Indice optique de la glace $𝑛_𝑔 = 1,31$
Masse volumique de la glace $𝜌_𝑔 = 0,917 × 10^3 kg.m^{−3}$
Masse volumique de l’eau liquide $𝜌_ℓ = 1,0 × 10^3 kg.m^{−3}$
Enthalpie massique de fusion de la glace $ℓ_𝑓 = 333,5 kJ.kg^{−1}$
Capacité thermique massique de l’eau liquide $𝑐_ℓ = 4,18 kJ.kg^{−1}.K^{−1}$
Rayon de la Terre $𝑅_𝑇 = 6 400 km$
Norme de l’accélération de la pesanteur $𝑔 = 9,8 m.s^{−2}$
1. Modélisation du halo solaire
I. La réfraction de la lumière
1. On considère un milieu homogène, isotrope et transparent à la lumière. Exprimer l’indice optique 𝑛 de ce milieu en fonction de la célérité 𝑣 de la lumière dans ce milieu et de la célérité 𝑐 de la lumière dans le vide.
L’indice optique représente la rapport entre la vitesse de la lumière dans le vide et celle dans le milieu, soit :
$n=\frac{c}{\nu}$
L’indice optique est toujours supérieur à 1.
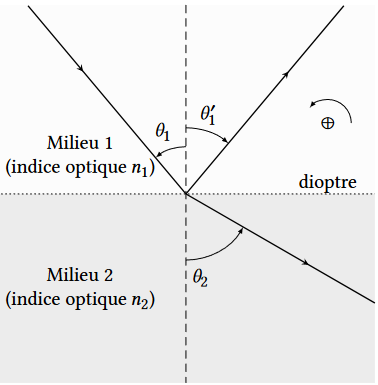
On étudie la situation, représentée sur la figure 1 suivante, de la réfraction et de la réflexion de la lumière.
Un rayon lumineux incident arrive sur un dioptre qui sépare deux milieux d’indices optiques $𝑛_1$ et $𝑛_2$.
On note $𝜃_1$ l’angle d’incidence du rayon incident, $𝜃′_1$ l’angle que le rayon réfléchi fait avec la normale
au dioptre, et $𝜃_2$ l’angle que le rayon réfracté fait avec cette même normale. Les angles considérés sont algébriques ; le sens positif, qui correspond au sens trigonométrique, est défini sur la figure 1 avec le symbole ⊕.
Figure 1 – Réflexion et réfraction de la lumière par un dioptre ($𝑛_2 < 𝑛_1$). Les différents angles sont orientés : $𝜃_1 > 0$, $𝜃′_1 < 0$ et $𝜃_2 > 0$. Le sens positif est le sens trigonométrique.
2. Rappeler les lois de la réflexion et de la réfraction de Snell-Descartes.
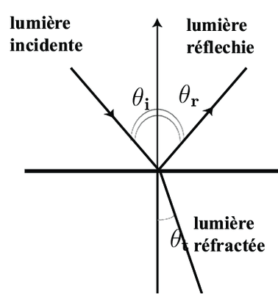Soit un rayon en incidence quelconque sur un dioptre séparant 2 milieux d’indice différents ($n_1$ et $n_2$). Ici nous ne donnons pas de sens aux angles.
Le rayon réfléchi, le rayon réfracté, le rayon incident et la normale (au dioptre) sont contenus dans le plan d’incidence.
Loi de la réflexion :
les angles incidents et réfléchis sont égaux $\theta_i = \theta_r$
Loi de la réfraction :
La relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incident θi et réfracté θt, appelée relation de Snell-Descartes, s’écrit :
$n_1 sin(\theta_i) = n_2 sin(\theta_t)$
3. Montrer que, dans le cas où $𝑛_2 < 𝑛_1$, si $𝜃_1$ est supérieur à une valeur $𝜃_ℓ$, l’énergie véhiculée par le rayon incident est totalement réfléchie par le dioptre. Nommer cette situation.
Si $n_2<n_1$ $\Rightarrow$ $\frac{n_2}{n_1}<1$, or $\frac{n_2}{n_1}=\frac{sin(\theta_1)}{sin(\theta _2)}<1$ $\Rightarrow$ $\theta_1 < \theta_2$ car sinus est une fonction croissante sur l’intervalle $[0:\frac{\pi}{2}]$
Il y a donc une valeur limite de $\theta_1$ au delà de laquelle l’onde est totalement réfléchie, on parle d’angle limite et de réflexion totale.
4. Exprimer $𝜃_ℓ$ en fonction de $𝑛_1$ et $𝑛_2$.
On a $\theta_l$ lorsque $\theta_2 = \frac{\pi}{2}$.
$n_1 sin(\theta_l)= n_2$ $\Rightarrow$ $\theta_l = arcsin(\frac{n_2}{n_1})$
5. Dans le cas d’un dioptre séparant la glace (milieu 1) de l’air (milieu 2), calculer la valeur de $𝜃_ℓ$ en degrés.
$\theta_l = arcsin(\frac{n_a}{n_g})$
Application Numérique :
$\theta_l = arcsin(\frac{1,00}{1,31})$ $=49,8°$
II. Le halo solaire
Le halo solaire, ou anthélie, est un phénomène optique atmosphérique qui ressemble à un arc-en-ciel circulaire (voir figure 2 à gauche). Il apparaît sous la forme d’un cercle coloré dont le soleil occupe le centre. L’objectif de cette sous-partie est la détermination du rayon angulaire du halo (qui représente l’angle au sommet du cône représenté sur la figure 2 à droite).
Le halo est dû à la réfraction de la lumière issue du soleil par de petits cristaux de glace en forme de bâtonnets. Les plus petits de ces cristaux (dont la taille peut être inférieure à 20 μm) ont un mouvement erratique provoqué par le choc des molécules qui constituent l’air ; ils ont donc toutes les orientations possibles dans l’espace. Puisqu’on ne s’intéresse qu’à la déviation des rayons lumineux, on peut modéliser la réfraction de la lumière issue du soleil par l’ensemble de ces cristaux par la réfraction de la lumière par un seul cristal en considérant un angle d’incidence variable.
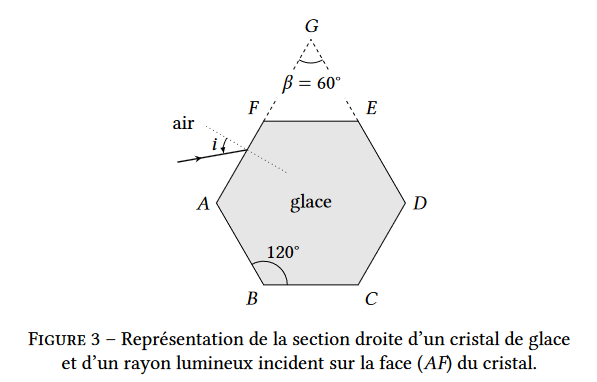
La figure 3 donne la représentation de la section droite d’un cristal de glace. Cette section présente la géométrie d’un hexagone régulier (𝐴𝐵𝐶𝐷𝐸𝐹). Un rayon lumineux incident, contenu dans le plan de cette section, atteint la face (𝐴𝐹 ) avec un angle d’incidence variable 𝑖. On étudie la déviation de ce rayon lumineux par le cristal.
6. Justifier que le rayon lumineux qui émerge du cristal ne peut pas sortir par la face (𝐸𝐹).
On sait qu’il peut exister un angle limite $\theta_l$ pour le lequel le rayon dans la glace ne sortira pas(réflexion totale).
On peut alors légitimement se poser la question de la valeur de l’angle i, doit il être petit ou grand ?
Analysons le schéma suivant :
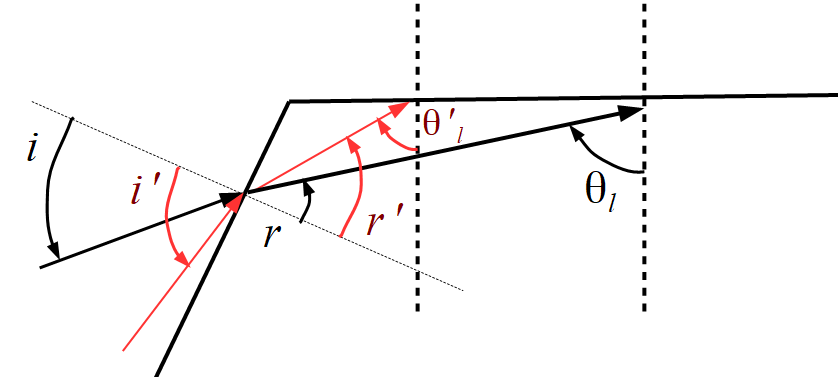
Si deux rayons entrent au même point avec $i’ > i$ alors $r’ > r$ car la fonction sinus est croissante sur l’intervalle $[0;\frac{\pi}{2}]$ et finalement $\theta_l > \theta_l’$
Or si on étudie le rayon qui donne un angle $\theta$ minimal et qu’il y a réflexion totale alors il n’est pas nécessaire d’étudier les angles $\theta_l$ supérieur car il y aura réflexion totale également.
Ici prendre l’angle $\theta_l$ le plus petit revient à prendre l’angle i le plus grand soit $\frac{\pi}{2}$
Pour retrouver la valeur de l’angle $\theta _{l,min}$ on utilise la propriété que dans un triangle, la somme des angles vaut 180°.
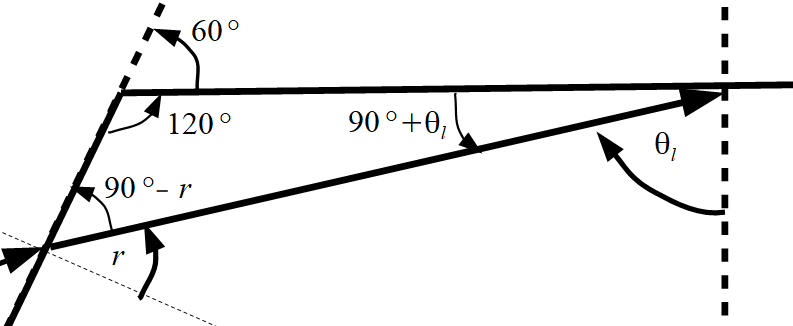
Attention ici à la convention du sens trigonométrique des angles. L’angle $\theta_l$ doit être négatif.
On retrouve :
$90-r+120+90 + \theta_l =180$
Soit $\theta_l = -120 + r$ avec $r=arcsin(\frac{n_a sin(\frac{\pi}{2})}{n_g})$
Application Numérique :
$\theta_l = -120 + arcsin(\frac{1 \times 1}{1,31})$ $= -70,2°$
L’angle limite est de -48,2°, on est donc bien au delà, il y a donc réflexion totale sur la face (EF)
7. Justifier qu’un rayon lumineux qui émerge par la face (𝐶𝐷) est parallèle au rayon lumineux incident et n’est donc pas dévié par le cristal de glace.
Traçons le parcours du rayon entrant en (AF) pour sortir en (CD) :
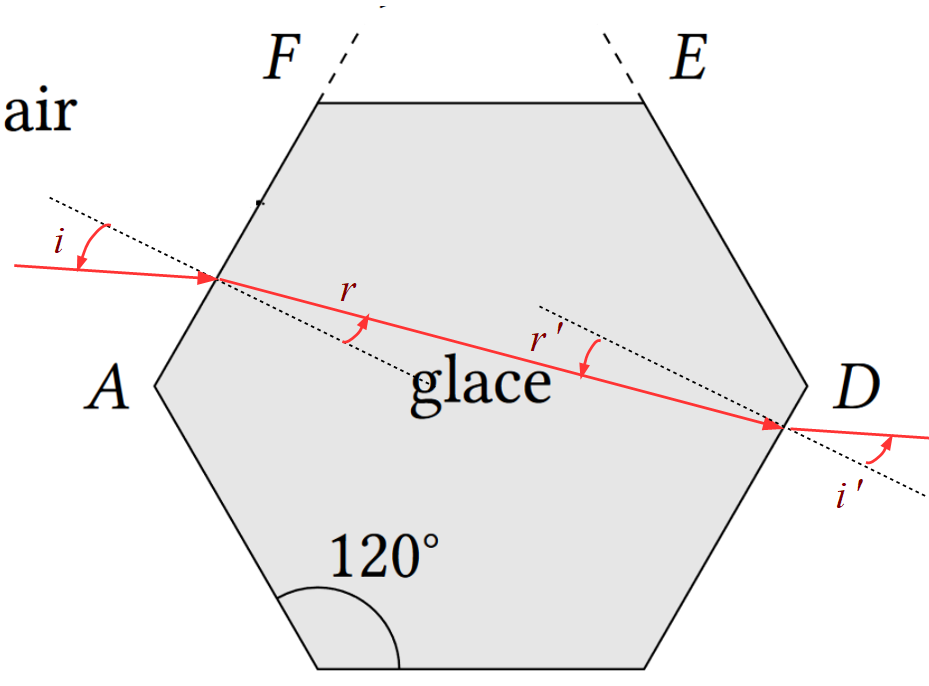
Les 2 faces (AF) et (CD) sont parallèles. Les normales à ces deux faces le sont également. Les angles r et r’ sont des angles alternes internes, ils sont donc égaux. r=r’.
Or à l’interface (AF) on a : $n_a sin(i) = n_g sin(r)$ et à l’interface (CD) on a : $n_g sin(r’) = n_a sin(i’)$
Comme $n_g sin(r) = n_g sin(r’)$ alors $n_a sin(i) = n_a sin(i’)$ soit $i=i’$
Le faisceau n’est donc pas dévié.
On considère le rayon émergent par la face (𝐷𝐸). Les faces (𝐴𝐹 ) et (𝐷𝐸) sont analogues aux faces d’un prisme de sommet 𝐺, d’angle au sommet 𝛽 égal à 60° et d’indice optique égal à celui de la glace, à savoir $𝑛_𝑔$ (voir figure 4).
Les différents angles sont définis sur la figure 4. On les oriente selon la convention suivante : les angles qui correspondent à une rotation dans le sens trigonométrique sont comptés positivement. Le sens trigonométrique est rappelé par une flèche courbe sur la figure 4, associée au symbole ⊕.
On note 𝛿 l’angle qui mesure la déviation du rayon incident après sa traversée du prisme. Les différents angles sur la figure 4 ont les signes suivants : 𝑖 > 0, 𝑟 > 0, 𝑖′ < 0, 𝑟′ < 0 et 𝛿 < 0.
8. Donner les relations qui lient 𝑖, 𝑟 et $𝑛_𝑔$ d’une part ; 𝑖′, 𝑟′ et $𝑛_𝑔$ d’autre part.
$sin(i) = n_g sin(r)$ car $n_a=1$
et
$n_g sin(r’) = sin(i’)$
9. Établir que : 𝛽 = 𝑟 − 𝑟′ et que 𝛿 = 𝑖 − 𝑟 + 𝑟′ − 𝑖′.
Pour $\beta$ :
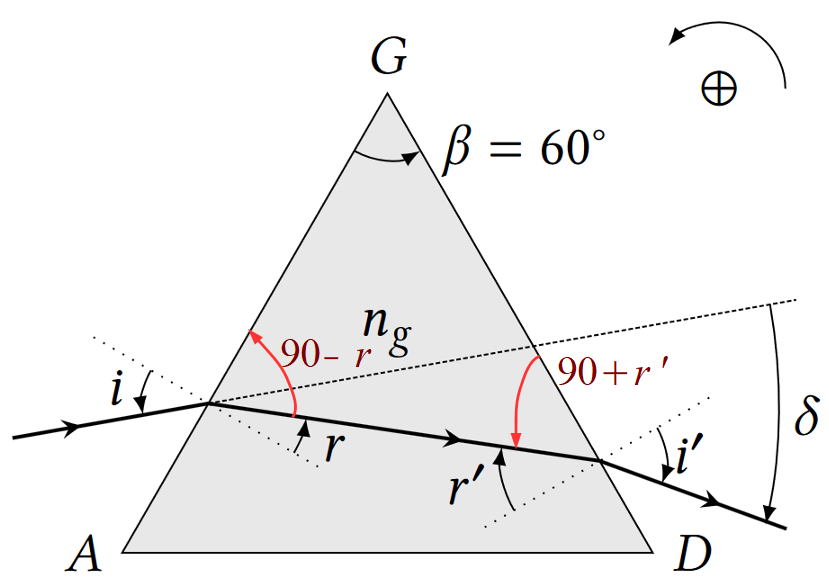
Attention au sens de l’angle, ici r’ est négatif. On retrouve un triangle dont la somme des angles vaut 180°.
$90 -r + \beta +90 +r’ = 180$ soit $\beta = r-r’$
Pour $\delta$ :
On observe déjà que $\delta$ est négatif. On peut décomposer la déviation en deux déviations $\delta_1 et \delta_2$.
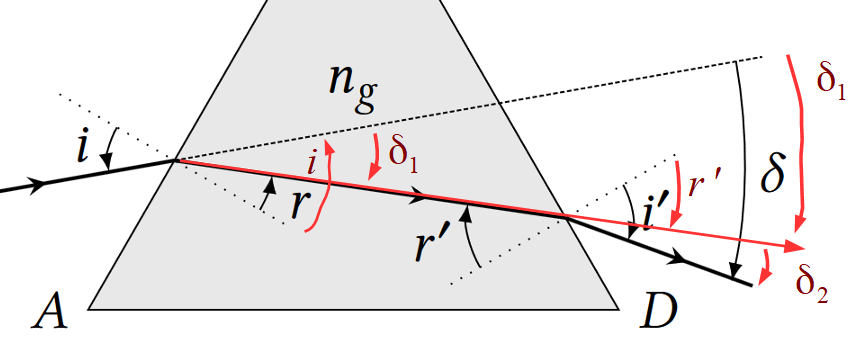
$\delta_1 = r-i <0$ et $\delta_2 = i’ – r’ <0 $
On a alors : $\delta = \delta_1 + \delta_2 $ $=r-i+i’-r’$
Ici il y a une erreur dans l’énoncé, on le voit particulièrement pour $\delta_1$, dans l’énoncé on nous propose $i-r$ or i et r sont tous les dans le sens positif et i>r ce qui donne $i-r>0$ pourtant on voit bien que sur le schéma $\delta_1 $ est négatif.
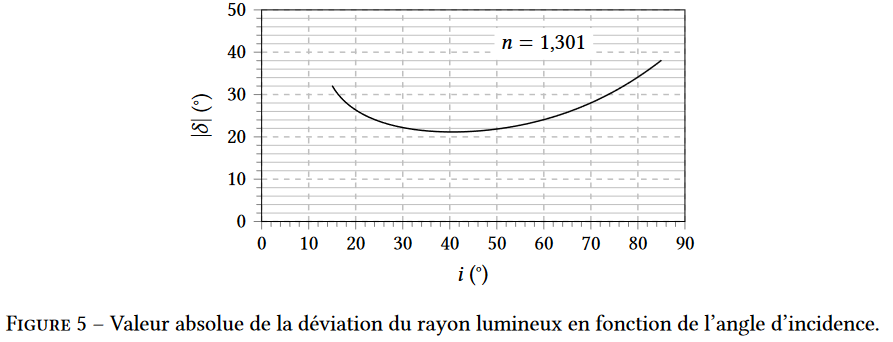
10. La figure 5 montre les variations de la valeur absolue de la déviation |𝛿| en fonction de l’angle d’incidence. On constate l’existence d’une valeur minimale dont on admet qu’elle est obtenue lorsque 𝑖 = −𝑖′. En déduire que dans cette configuration : 𝑟 = 𝛽/2 et $sin 𝑖 = 𝑛_𝑔 sin(𝛽/2)$ .
Si $i=-i’$ cela implique que $r=-r’$ donc $\beta = 2r$ $\Rightarrow r=\frac{\beta}{2}$
De plus, d’après la loi de Snell-Descartes : $n_a sin(i) = n_g sin(r)$ $\Rightarrow$ $sin(i) = n_g sin(\frac{\beta}{2})$
11. La figure 5 montre que la valeur minimale de |𝛿| est approximativement égale à 22°. Retrouver ce résultat par le calcul.
On a $r= \frac{\beta}{2} = 30°$ et $sin(i) = n_g sin(\frac{\beta}{2})$ donc $i= arcsin(n_g sin(\frac{\beta}{2})$
Application Numérique :
$i= arcsin(1,301 sin(\frac{60}{2}))$ $\simeq 41°$
On peut retrouver $\delta = 2i – 2r$
Application Numérique :
$\delta = 2 \times 41 – 2 \times 30$ $=22°$
12. Expliquer pourquoi l’observateur observe une accumulation de lumière (le halo solaire) dans la direction qui correspond à une ouverture angulaire de 22° autour de l’axe dirigé de son œil vers le Soleil.
Sur la figure 5, la déviation autour de 22° est obtenue pour une large gamme d’angle du rayon incident (i allant de 30° à 50°). La répartition de l’intensité lumineuse se fait alors plus importante dans cette direction.
13. L’indice optique de la glace est une fonction décroissante de la longueur d’onde. On observe que le halo solaire est irisé (l’irisation est la production des couleurs de l’arc-en-ciel par décomposition de la lumière du soleil) : de l’intérieur vers l’extérieur du halo, les couleurs observées varient du rouge au bleu. Préciser si les résultats établis précédemment sont en accord avec cette observation.
L’indice optique est une fonction décroissante de la longueur d’onde.
On a : $\lambda _{rouge}> \lambda_{bleu}$ $\Rightarrow$ $n_{rouge}<n_{bleu}$
Dans la glace, si $n_g$ augmente alors r diminue car $r=arcsin(\frac{sin(i)}{n_g})$ et arcsin est une fonction croissante, r varie en $arcsin(\frac{1}{r})$
Si r diminue alors r’ augmente car $\beta = r – r’ = 60°$
et si r’ augmente alors i’ augmente (Loi de Snell Descartes).
On en conclut que pour les indices élevés la déviation est plus grande, donc la déviation du bleu est plus importante que celle du rouge. La démonstration est en accord avec l’observation.
2. La fonte des inlandsis
Un inlandsis est un glacier de grande étendue qui se présente sous la forme d’une couche de glace dont l’épaisseur peut atteindre plusieurs milliers de mètres et qui recouvre le sol. Il n’existe sur Terre que deux inlandsis : celui du Groënland et celui de l’Antarctique. Ces deux inlandsis se prolongent vers la mer ou l’océan sous la forme de barrières de glace, dont se détachent les icebergs.
On propose d’abord dans cette partie d’estimer la hausse du niveau des océans sur Terre qui résulte de la fonte des inlandsis ou de la fonte des icebergs. Dans la dernière sous-partie est abordé l’aspect énergétique de la fusion de la glace, tel qu’il peut être étudié en séance de travaux pratiques.
I. Équilibre hydrostatique d’un glaçon dans l’eau liquide
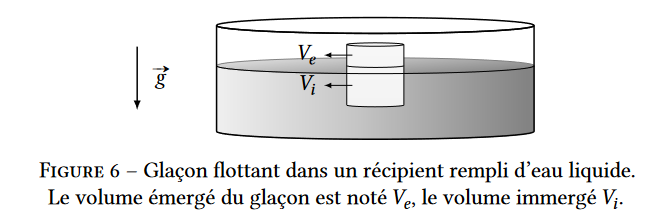
Afin d’analyser l’éventuel impact de la fonte des icebergs sur l’élévation du niveau des océans, on propose d’étudier une situation modèle. On considère l’équilibre d’un glaçon, constitué d’eau pure, dans un récipient contenant de l’eau liquide (voir figure 6).
14. Donner l’expression de la poussée d’Archimède $\vec Π$ que l’eau liquide exerce sur le glaçon en fonction du volume immergé $𝑉_𝑖$, de la masse volumique $𝜌_ℓ$ de l’eau liquide et de l’accélération de la pesanteur $\vec 𝑔$ .
$\vec \Pi = – \rho_l V_i \vec g$
15. Rappeler la nature des actions mécaniques à l’origine de la poussée d’Archimède.
Les actions mécaniques à l’origine de la poussée d’Archimède sont les forces pressantes exercées par l’eau sur la face inférieure du glaçon et plus précisément la différence de force pressante entre le haut de l’objet immergé et le bas.
16. On fait l’hypothèse que la poussée d’Archimède exercée par l’air est négligeable devant celle exercée par l’eau. Préciser néanmoins le sens de la poussée d’Archimède exercée par l’air sur le glaçon.
L’air exerce une pression sur la partie latérale du glaçon qui se compense de chaque coté et donc s’annule.
L’air exerce également une force pressante sur le dessus du glaçon qui n’est pas compensé. On a donc une poussée exercée par l’air sur le glaçon orienté vers le bas.
17. Exprimer le volume émergé $𝑉_𝑒$ en fonction du volume immergé $𝑉_𝑖$ et des masses volumiques de l’eau liquide $𝜌_ℓ$ et de la glace $𝜌_𝑔$.
On applique le principe fondamental de la dynamique : $\sum \vec F = m \vec a = \vec 0$
$\vec P + \vec \Pi = \vec 0$ $\Rightarrow$ $m \vec g – \rho_l V_i \vec g = \vec 0$
$m=\rho_l V_i$, or $m=\rho_g V_{tot}$ avec $V_{tot}= V_i + V_e$
$\Rightarrow$ $\rho_l V_i = \rho_g (V_e + V_i)$ $\Rightarrow$ $V_e=V_i[\frac{\rho_l}{\rho_g}-1]$
On repère le niveau de l’eau liquide dans le récipient juste après avoir déposé le glaçon et juste après la fonte de celui-ci.
18. Justifier que le niveau d’eau liquide dans le récipient ne varie pas après la fonte du glaçon.
Ici il faut démontrer que le volume qu’occuperait l’eau issue de la totalité de la fonte du glaçon $V_{l,fus}$ correspond au volume $V_i$ occupé par le glaçon.
$V_{l,fus}= \frac{m_g}{\rho_l}$ $=\frac{\rho_g V_{tot}}{\rho_l}$ $=\frac{\rho_g (V_i + V_e)}{\rho_l}$ or $V_e=V_i[\frac{\rho_l}{\rho_g}-1]$ (q.17) donc :
$=\frac{\rho_g (V_i + V_i[\frac{\rho_l}{\rho_g}-1])}{\rho_l}$ $=\frac{\rho_g}{\rho_l} \times \frac{\rho_l}{\rho_g} \times V_i $ $= V_i$
19. Préciser si ce résultat se maintient dans le cas où le glaçon constitué d’eau pure flotte dans de l’eau salée, de masse volumique supérieure à celle de l’eau pure.
On a le même glaçon donc la même masse et le même volume d’eau lorsqu’il a fondu. Or comme il était plongé dans un milieu plus dense, le volume immergé est plus petit car le produit $\rho_l \times V_i$ reste constant.
On a donc une montée de l’eau lors de la fonte de la glace d’eau pure dans une eau salée.
20. Conclure quant à l’éventuelle contribution de la fonte des icebergs à l’élévation du niveau des océans.
Les icebergs sont constitués d’eau douce et flottent dans de l’eau salée, on se retrouve dans la même configuration que la question précédente. Lorsque l’iceberg fond il fait augmenter le niveau des océans.
II. Hausse du niveau des océans due à la fonte des inlandsis.
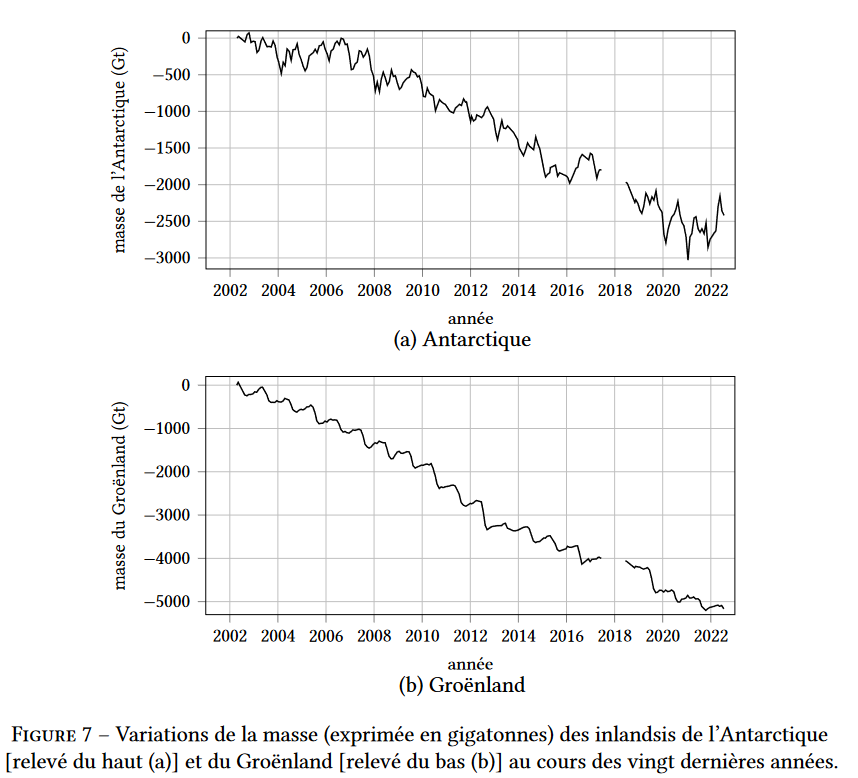
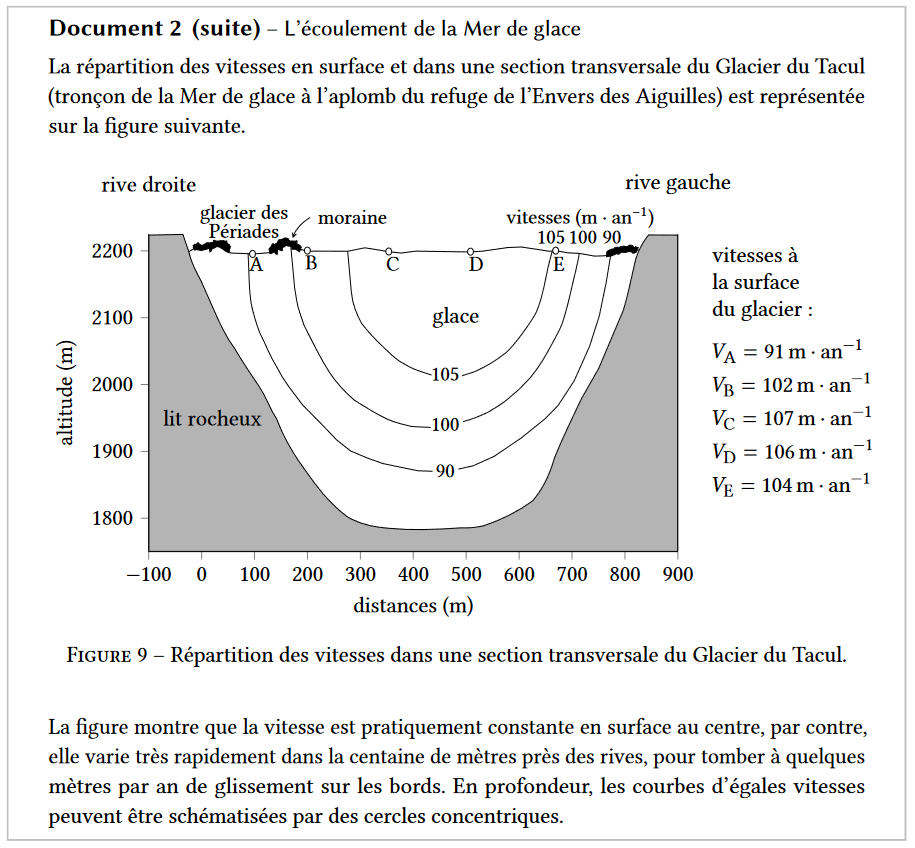
La fonte de la glace qui constitue les inlandsis contribue à l’élévation du niveau des océans. Les variations de l’épaisseur moyenne des inlandsis se déduisent des mesures de leur altitude de surface par des satellites dédiés. La figure 7 représente les variations estimées de la masse des inlandsis de l’Antarctique et du Groënland depuis 2002.
21. Les relevés de la figure 7 présentent des oscillations particulièrement visibles dans le cas du Groënland (graphique (b) à droite de la figure). Estimer grossièrement la période de ces oscillations et proposer une interprétation de leur origine.
On observe 2 oscillations par an soit une période de 6 mois. Cela est du aux périodes hiver/été. L’hiver la glace se reforme et l’été elle fond.
22. Estimer la hausse du niveau des océans consécutive à la fonte des inlandsis du Groënland et de l’Antarctique pendant les vingt dernières années, en s’appuyant sur les données de la figure 7.
Sur la figure a) on perd environ $2700 Gt$ de glace et sur la figure b) on perd $5100Gt$ de glace soit au total 7800Gt.
La masse perdue est de $m=7,8.10^{15}kg$, ce qui correspond à un volume de $V=\frac{m}{\rho_g}$ $=8,5.10^{12}m^3$
Calcul de la surface de la Terre :
$S_{terre}=4 \pi R_t^2$ $=5,15.10^{14}m^2$
On retrouve la hauteur en considérant que l’eau recouvre 70% de la surface de la Terre correspondant aux océans.
$V =\frac{70}{100} \times S_{Terre} \times h$ $\Rightarrow$ $h=\frac{V}{\frac{70}{100} S_{Terre}}$ $=23,6cm$ soit 1,2cm/an.
III. Détermination expérimentale de l’enthalpie massique de fusion de la glace.
On propose dans cette sous-partie d’analyser les résultats expérimentaux obtenus par des étudiants à l’occasion d’une séance de travaux pratiques ayant pour but la détermination de la valeur de l’enthalpie massique de fusion de la glace.
23. Rappeler la définition de l’enthalpie massique de fusion de la glace.
L’enthalpie massique de fusion de la glace est l’énergie nécessaire absorbé par la glace par unité de masse pour passer de l’état solide à l’état liquide.
La démarche expérimentale suivie pour déterminer l’enthalpie massique de fusion de la glace met en œuvre une technique calorimétrique particulière, la méthode des mélanges. Le protocole est détaillé dans le document 1, qui donne aussi toutes les indications utiles sur l’affichage des valeurs mesurées par les appareils utilisés.
Document 1 – Détermination de l’enthalpie massique de fusion de la glace par la méthode des mélanges
Protocole
1. Introduire une masse $𝑚_1$ d’eau liquide connue (procéder à une pesée) dans le calorimètre.
2. Une fois l’équilibre thermique atteint, repérer la température $𝜃_1$ de l’eau (et donc du calorimètre).
3. Prélever 5 ou 6 glaçons et les placer dans un verre à pied et mesurer leur masse $𝑚_2$.
4. Attendre que les glaçons commencent à fondre et suivre leur température $𝜃_2$.
5. Lorsque le thermomètre indique que la température des glaçons est $𝜃_2 = 0 °C$, les introduire rapidement dans le calorimètre.
6. Une fois que les glaçons ont fondu et que l’équilibre thermique est atteint, repérer la température finale $𝜃_𝑓$ du système.
Résolution des appareils de mesure
• les masses sont mesurées à l’aide d’une balance électronique qui affiche la valeur de la masse au gramme près. On assimile la valeur mesurée d’une masse à une variable aléatoire suivant une loi uniforme sur un intervalle de largeur égale à un gramme, centré sur la valeur affichée par la balance.
• les températures sont repérées à l’aide d’un thermomètre électronique qui mesure et affiche la valeur de la température au dixième de degré Celsius près. On assimile la valeur mesurée d’une température à une variable aléatoire suivant une loi uniforme sur un intervalle de largeur égale à un dixième de degré Celsius, centré sur la valeur affichée par le thermomètre.
Les résultats obtenus par un groupe d’étudiants sont les suivants :
$𝑚_1 = 250 g$ $𝑚_2 = 32 g$
$𝜃_1 = 18,7 °C$ $𝜃_2 = 0,0 °C$
$𝜃_𝑓 = 9,7 °C$
24. En supposant que le système {eau+glaçons} évolue de façon adiabatique, établir, à l’aide d’un bilan énergétique, la relation suivante :
$ℓ_𝑓 = − \frac{𝑚_1}{𝑚_2}𝑐_ℓ(𝜃_𝑓 − 𝜃_1) − 𝑐_ℓ(𝜃_𝑓 − 𝜃_2) $.
Bilan d’enthalpie :
$\Delta H = \Delta H_{fus} + \Delta H_{glace} + \Delta H_{eau} = 0$ car le système évolue de façon adiabatique.
$\Delta H_{glace}$ : énergie nécessaire pour faire passer l’eau liquide issue de la glace de la température 0°C à la température finale.
$\Delta H_{eau}$ : énergie nécessaire pour faire passer l’eau liquide de la température 18,7°C à la température finale.
$m_2 l_f + m_2 c_l (\theta _f – \theta_2)+ m_1 c_l (\theta_f – \theta_1)=0 $
$\Rightarrow$ $ℓ_𝑓 = − \frac{𝑚_1}{𝑚_2}𝑐_ℓ(𝜃_𝑓 − 𝜃_1) − 𝑐_ℓ(𝜃_𝑓 − 𝜃_2) $
Afin d’exploiter le résultat de leurs mesures et de prendre en compte les incertitudes de mesure, les étudiants rédigent et utilisent le programme python suivant :
1 ## importation des bibliothèques
2 import numpy as np
3 import numpy.random as rd
4
5 ## Constantes physiques
6 # Capacité thermique massique de l’eau liquide
7 c = 4.18E3
8
9 ## fonctions définies par l’utilisateur
10 def lf(m1,m2,Tf,Te,Tg):
11 »’
12 Renvoie la valeur de lf à partir de
13 – masse d’eau liquide m1 à température initiale Te (en K)
14 – masse de glace m2 à température initiale Tg (en K)
15 – température finale Tf (en K)
16 »’
17 return -(m1/m2)*c*(Tf-Te)-c*(Tf-Tg)
18
19 def calcul_lf(N, m1, m2, Tf, Te, Tg, delta_m, delta_T):
20 »’
21 Renvoie la valeur de l’enthalpie massique de fusion et calcule l’incertitude-type
22 par la méthode de Monte-Carlo, étant donné les valeurs des grandeurs utiles et
23 les largeurs de leurs intervalles de variation. Ces grandeurs sont considérées comme
24 des variables aléatoires avec une loi de probabilité uniforme sur ces intervalles de variation.
25 »’
26 # Création d’un tableau vide contenant N termes
27 liste = np.empty(N)
28 # tirage aléatoire des valeurs des grandeurs (méthode de Monte-Carlo)
29 for i in range(N):
30 me_sim = m1 + (delta_m/2)*rd.uniform(-1,1)
31 mg_sim = m2 + (delta_m/2)*rd.uniform(-1,1)
32 liste[i] = lf(me_sim,mg_sim,Tf,Te,Tg)
33 return [np.mean(liste),np.std(liste)]
34 a=10000
35 resultat = calcul_lf(100000, 0.250, 0.032, 282.7, 291.7, 273.0, 0.001, 0.1$)
36 print(« Moyenne = %.2f kJ/kg ; écart-type = %.2f kJ/kg »%(resultat[0]/1000, resultat[1]/1000))
25. Expliquer pourquoi ce programme, bien que sa syntaxe soit correcte, ne fournit pas une valeur satisfaisante de l’incertitude-type sur la mesure de l’enthalpie massique de fusion de la glace.
La méthode Monte-Carlo nécessite d’utiliser l’incertitude type en $\frac{\Delta}{\sqrt{3}}$, on aurait les lignes 30 et 31 qui doivent être :
30 me_sim = m1 + (delta_m/sqrt(3))*rd.uniform(-1,1)
31 mg_sim = m2 + (delta_m/sqrt(3))*rd.uniform(-1,1)
Une fois l’erreur corrigée, le programme fournit le résultat suivant :
1. Moyenne = 253.38 kJ/kg ; écart-type = 3.03 kJ/kg
26. En s’appuyant sur le calcul d’un écart normalisé, comparer la valeur obtenue pour $ℓ_𝑓$ à la valeur de référence donnée dans le tableau de valeurs numériques en début du sujet (page 2).
On calcule l’écart normalisé grâce à la formule suivante :
$E_N = \frac{\lvert {l_{f1}-l_f}\rvert}{u(l_f)}$
Application Numérique :
$E_N = \frac{\lvert {333,5-253,38}\rvert}{3,03}= 26,44$
On trouve un écart normalisé important ce qui implique des résultats incompatibles.
27. Proposer une critique succincte du protocole suivi.
Le protocole suppose que l’échange thermique ne vient que du mélange entre les glaçons et l’eau du calorimètre. Or l’écart principal entre la mesure et la théorie vient de l’étape où les glaçons sont placés dans le verre à pied. Lors de la fonte des glaçons les parois du verre ainsi que l’air échange de l’énergie avec les glaçons. C’est principalement cet échange d’énergie qui est la cause de l’écart important des résultats.
On peut également comprendre cette différence en raisonnant sur la masse de la glace $m_2$. Le calcul de la chaleur latente se fait en gardant cette masse mesurée en tout début de protocole, or la glace fond et la masse de glace diminue, ce n’est plus une masse $m_2$ que l’on place dans le calorimètre mais une masse plus faible.
D’où le résultat en dessous de ce qui est attendu.
3. Quelques propriétés hydrodynamiques des glaciers
Du fait de leur plasticité, les glaciers s’écoulent lentement sous l’effet de la gravité avec une vitesse d’écoulement très variable selon la pente, la topographie du lit rocheux ou l’épaisseur de la glace. La vitesse moyenne est de l’ordre de quelques centimètres à quelques dizaines de centimètres par jour, le record revenant au glacier Kangerdlugssuaq dans le Groënland où la vitesse moyenne atteinte est de 14 kilomètres par an. Par ailleurs, les glaciers ne sont pas des masses compactes de glace. Ils sont traversés par un réseau hydrographique de canaux qui collectent et véhiculent l’eau liquide formée en surface.
Cette partie propose d’étudier, sur la base du modèle de Poiseuille, l’écoulement d’un glacier sous l’effet de la gravité et d’interpréter certains aspects du réseau hydrographique interne au glacier grâce au modèle de Roethlisberger.
I. L’écoulement de Poiseuille dans une conduite cylindrique.
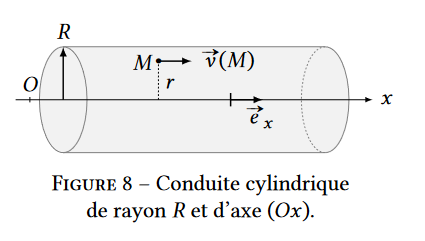
On considère l’écoulement stationnaire d’un fluide visqueux newtonien de viscosité dynamique 𝜂, incompressible de masse volumique 𝜌, dans une conduite cylindrique horizontale de rayon 𝑅 et d’axe de symétrie de révolution (𝑂𝑥). Il règne dans la conduite un gradient horizontal de pression noté $\frac{dp}{dx}$ (avec $\frac{dp}{dx}$ < 0), supposé indépendant de 𝑥. En un point 𝑀 de l’écoulement, la vitesse d’écoulement du fluide s’écrit : $\vec{v} (M) = v(r) \vec e_x$, où 𝑟 est la distance entre le point 𝑀 et l’axe (𝑂𝑥) et $\vec{e_x}$ un vecteur unitaire orientant l’axe (𝑂𝑥) (voir figure 8).
On admet que le fluide adhère aux parois de la conduite, ce qui se traduit par : 𝑣(𝑟 = 𝑅) = 0.
28. À l’aide d’un bilan de quantité de mouvement appliqué à un système fermé à définir, établir l’expression suivante de la vitesse d’écoulement, en prenant soin d’expliciter chaque étape du raisonnement :
$\vec{v} (M)= \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} \vec e_x$ (1)
La force de viscosité $\vec 𝑓_v$ que le fluide situé à l’extérieur du cylindre de rayon $𝑟$, de longueur $𝐿$ et d’axe $(𝑂𝑥)$ exerce sur le fluide contenu dans ce cylindre s’écrit : $\vec f_v = 2 \pi r L \eta \frac{dv}{dr} \vec e_x$
On considère la portion de fluide cylindrique, de rayon r et de longueur dx, centrée sur l’axe.
On note $P_e$ la pression à l’entrée de cette portion de fluide et $P_s$ la pression en sortie. Soit $dp = P_s – P_e)$
On applique le théorème de la résultante cinétique au système constitué de cette portion de fluide à l’instant $t$ et de la masse $dm$ qui y rentre entre les instants $t$ et $t + dt$.
A l’instant $t + dt$, ce système est constitué de la même portion de fluide contenu dans le cylindre de rayon $r$ et de la masse $dm$ qui en est sortie entre les instants $t$ et $t + dt$.
En régime stationnaire, la variation de quantité de mouvement de ce système fermé est alors simplement nulle.
Par conséquent, la somme des forces qui s’exercent sur ce système est également nulle :
$\sum{\vec F} = \vec 0$
Soit la force de pression en amont, $\pi r^2 P_e$, moins la force de pression en aval, $\pi r^2 P_s$ plus la force de frottement visqueuse F qui s’exerce sur la surface latérale du cylindre de rayon r qui est égale à 0 :
$\pi r^2 P_e – \pi r^2 P_s + F = 0$
Pour un fluide visqueux newtonien, la force de viscosité F est donnée par:
$F = \eta \frac{d v(r)}{dr} 2 \pi r dx$
On en déduit :
$\pi r^2 P_e – \pi r^2 P_s $$+ \eta \frac{d v(r)}{dr} 2 \pi r dx= 0$
Ce qui permet d’isoler la dérivée :
$\frac{dv(r)}{dr} = – \frac{P_e – P_s}{2 \eta dx} r$ $=\frac{dp}{2 \eta dx}r$
On intègre par rapport au rayon (dans ce cas dp/dx est constant) et on obtient :
$v(r)= \frac{dp}{2 \eta dx} \frac{r^2}{2}+cte$
La constante est obtenue connaissant v(r=R)=0.
$v(R)= 0=\frac{dp}{2 \eta dx} \frac{R^2}{2}+cte$ $\Rightarrow$ $cte = – \frac{dp}{2 \eta dx} \frac{R^2}{2}$
Soit :
$v(M)= \frac{dp}{2 \eta dx} \frac{(r^2 – R^2)}{2}$
29. En déduire l’expression du débit de volume $𝑄$ en fonction de $𝑅, 𝜂 et \frac{d𝑝}{d𝑥}$.
On ne peut pas utiliser la formule $Q=v \times S$ car la vitesse n’est pas constante sur la surface. Il faut alors revenir à la formule locale :
$Q=\iint _S \vec v (M) \vec{dS}$ avec $dS=r d \theta dr$
Soit : $Q=\iint _S v (M) r d \theta dr$ $=\iint _S \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r d \theta dr$ $=\int_{0}^{2 \pi} d \theta \int_{0}^{R} \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r dr$ $=2\pi \int_{0}^{R} \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r dr$ $=\frac{2 \pi}{4 \eta} \frac{dp}{dx} \int_{0}^{R} (r^3 -R^2 r)dr$ $=\frac{ \pi}{2 \eta} \frac{dp}{dx} [(\frac{r^4}{4} – R^2\frac{r^2}{2})]_{0}^{R} $ $=\frac{ \pi}{2 \eta} \frac{dp}{dx} [\frac{R^4}{4} – \frac{R^4}{2}]$ $= – \frac{\pi R^4}{8 \eta} \frac{dp}{dx}$
30. En déduire la dimension de la viscosité dynamique 𝜂 en fonction des dimensions fondamentales suivantes : longueur, masse et temps.
On a $\eta \# \frac{R^4 }{Q } \frac{dp}{dr}$ $= \frac{[L]^4}{\frac{[L]^3}{[T]}} \frac{[M].[L]^{-1}.[T]^{-2}}{[L]}$ $=\frac{[M]}{[L].[T]}$
II. Modélisation de l’écoulement de la Mer de glace
On choisit de modéliser l’écoulement de la Mer de glace par l’écoulement de Poiseuille stationnaire d’un fluide visqueux newtonien incompressible s’écoulant dans la moitié inférieure d’une conduite cylindrique sous le seul effet de la gravité, ce qui impose de remplacer dans l’expression (1) de la vitesse d’écoulement $\frac{dp}{dx}$ par $−𝜌_𝑔 𝑔 sin 𝛼$, où $𝜌_𝑔$ est la masse volumique de la glace, $𝑔$ la norme de l’accélération de la pesanteur et $𝛼$ l’angle qui mesure la pente moyenne de la Mer de glace.
31. À partir d’une analyse de la figure 9, proposer au moins un argument en faveur et au moins un argument en défaveur de ce choix de modélisation de l’écoulement du glacier par un écoulement de Poiseuille.
Argument en faveur : On observe bien une diminution de la vitesse lorsque l’on s’éloigne du centre en surface caractéristique d’un écoulement de Poiseuille. Que ce soit sur les bords ou en profondeur.
Argument en défaveur : La forte diminution de la vitesse sur les 100 derniers mètres ne sont pas compatibles avec un écoulement de Poiseuille.
32. En utilisant les données quantitatives disponibles dans le document 2 et en particulier sur la figure 9, proposer une estimation de l’ordre de grandeur de la viscosité dynamique de la glace. Comparer l’ordre de grandeur obtenu avec la valeur estimée usuelle de la viscosité de la glace de l’ordre de $10^{13} Pa⋅s$. Commenter.
D’après la formule (1) on a : $v(M)= \frac{(r^2 – R^2)}{4 \eta} (- \rho _g g sin \alpha)$ soit $\eta= \frac{(r^2 – R^2)}{4 v(M)} (- \rho _g g sin \alpha)$
Pour le calcul on prends le point E ($v_E$ est donné) on le situe à 200m du centre en surface.
Application Numérique :
$\eta= \frac{(200^2 – 400^2)}{4 \frac{104}{365\times 24 \times 3600}} (- 917 \times 9,81 sin 11)$ $=1,56.10^{13} Pa.s$
Malgré la non symétrie du profile des vitesses, on retrouve une valeur de la viscosité dynamique très proche de la valeur usuelle.
III. Modèle de Röthlisberger du drainage de l’eau liquide dans un glacier
L’eau liquide provenant de la fonte glaciaire et des précipitations est collectée en surface du glacier et pénètre en son sein. L’eau émerge au terminus du glacier par un petit nombre de conduits incisés à sa base. Il est tentant de supposer que ces conduits se prolongent dans la profondeur du glacier, le long de sa base.
Un conduit isolé rempli d’eau à l’intérieur du glacier a tendance à se refermer sous l’effet de la pression qu’exerce la glace environnante, à moins que l’écoulement de l’eau dans le conduit ne dissipe suffisamment d’énergie pour faire fondre les parois du conduit et le maintenir ainsi ouvert. Röthlisberger a a présenté la première analyse hydraulique et thermodynamique de l’écoulement stationnaire dans un canal de drainage, communément appelé canal de Röthlisberger.
a. Röthlisberger, H. 1972. Water pressure in intra- and subglacial channels. J. Glaciol., 11(62), 177-203.
On propose dans cette sous-partie d’interpréter la possibilité d’une arborescence des canaux de drainage.
On considère un canal de drainage cylindrique horizontal, d’axe (𝑂𝑥), de rayon $𝑅$, dans lequel s’écoule de l’eau, assimilée à un fluide newtonien incompressible, en régime stationnaire. La température et la pression de l’eau liquide en écoulement dans le canal dépendent de l’abscisse $𝑥$. On note respectivement $𝑇(𝑥)$ et $𝑝(𝑥)$ les champs de température et de pression correspondants. L’écoulement de l’eau s’effectue dans le sens des $𝑥$ croissants sous l’effet du gradient de pression $\frac{dp}{dx}$. Le débit de volume associé est noté $𝑄$.
Röthlisberger fait l’hypothèse que la puissance dissipée par viscosité dans l’écoulement permet non seulement d’éroder le canal par fusion des parois de glace mais aussi de maintenir en tout point du canal l’équilibre thermodynamique entre la glace et l’eau liquide.
33. On considère le système constitué de la masse de glace de la paroi du canal comprise entre les rayons $𝑅$ et $𝑅 + d𝑅$ et entre les abscisses $𝑥$ et $𝑥 + d𝑥$. En raison de la dissipation d’énergie par frottement visqueux dans l’écoulement, cette masse fond pendant la durée $d𝑡$. Exprimer la variation d’enthalpie $d𝐻_𝑔$ du système qui résulte de la fusion de la masse de glace considérée entre les instants $𝑡$ et $𝑡 + d𝑡$ en fonction de $𝑅$, $d𝑅$, $d𝑥$, $ℓ_𝑓$ (enthalpie massique de fusion de la glace) et $𝜌_𝑔$.
Déterminons tout d’abord la masse $dm$ de glace contenue dans le volume défini dans l’énoncé.
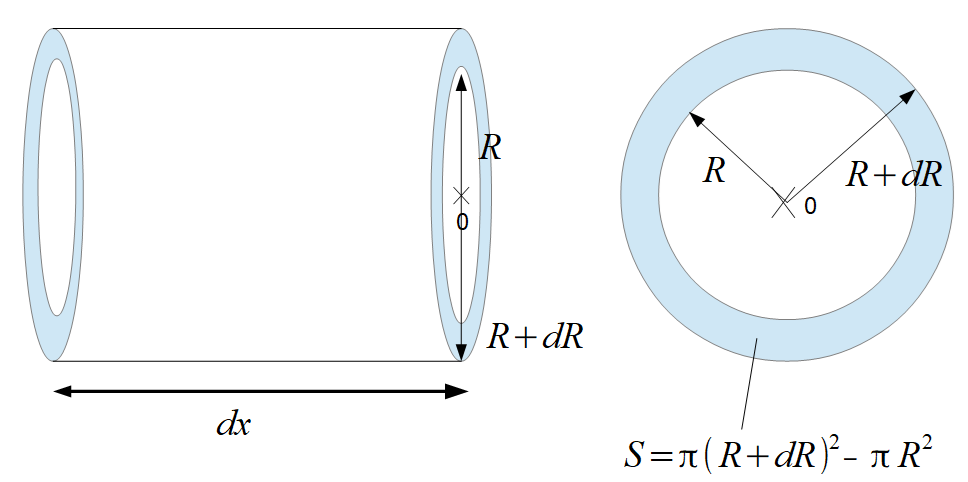
$dm = \rho_g dV = \rho_g dx \times S$ $= \rho_g dx [\pi (R+dR)^2 – \pi R^2]$ $= \rho_g dx [\pi dR^2 + 2 \pi RdR]$ $\simeq \rho_g dx 2 \pi RdR$ car $dR^2 << 2RdR$
La variation d’enthalpie est définie par : $dH_g = dm l_f$ $\simeq \rho_g dx 2 \pi RdR l_f$
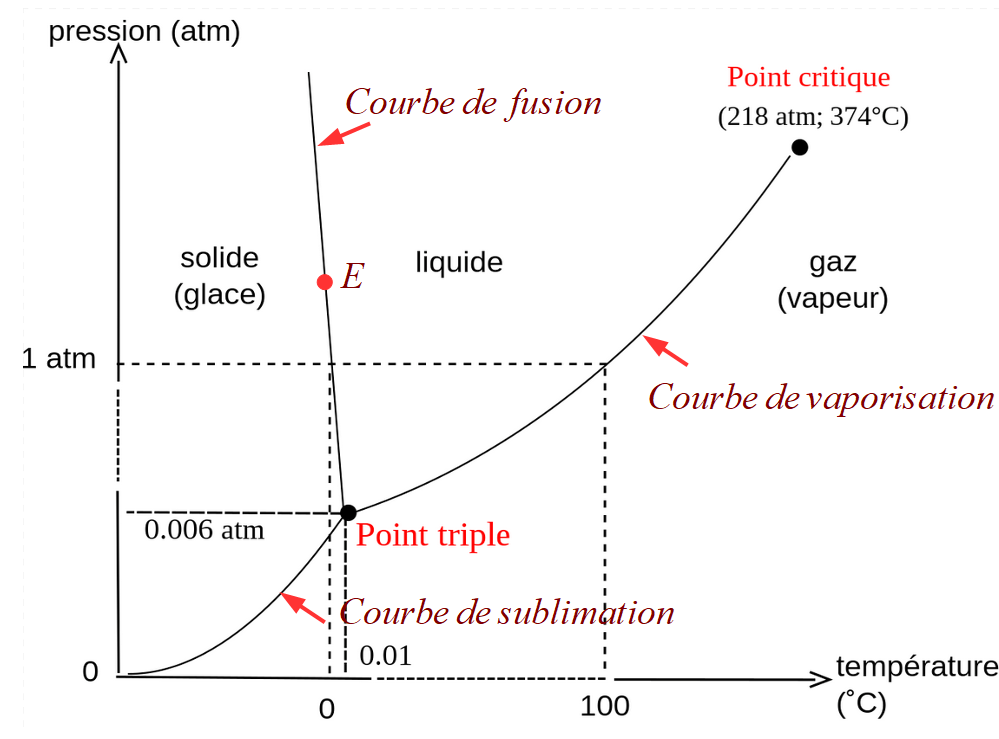
34. Identifier dans un diagramme pression-température les domaines de stabilité des phases liquide, gazeuse et solide de l’eau, et les délimiter en représentant leurs frontières. Placer le point triple 𝑌 et le point critique 𝐶 sur le diagramme. Placer également un point 𝐸, représentatif d’un équilibre thermodynamique entre l’eau liquide et la glace.
35.On considère le système fermé constitué, à l’instant $𝑡$, de l’eau qui se situe dans le volume du canal compris entre les abscisses $𝑥$ et $𝑥 + d𝑥$ et de l’eau qui entre dans ce volume pendant la durée $d𝑡$. Montrer, en explicitant soigneusement le raisonnement, que la variation d’enthalpie $d𝐻_ℓ$ de ce système fermé, entre les instants $𝑡$ et $ 𝑡 + d𝑡$ s’écrit :
$dH_l = \rho _l Q c_l \frac{dT}{dx} dx dt$ (2)
Nous étudions la variation d’enthalpie de 2 masses d’eau, l’une dans le système fermé et l’autre arrivant dans le système pendant $dt$. Or nous sommes en régime permanent et les variations temporelles dans un système fermé sont nulles. Il nous faut alors étudier la variation d’enthalpie de l’eau entrante dans le système pendant $dt$.
de plus dans les conditions de température les valeurs des capacités thermiques massiques à volume constant $c_V$ et à pression constante $c_P$ sont similaires.
Par définition : $c_P = \frac{1}{dm} (\frac{dH_l}{dT})_P = c_l$
$\Rightarrow$ $dH_l = dm c_l dT$ $= \rho_l dV c_l dT$
Pour le volume élémentaire :
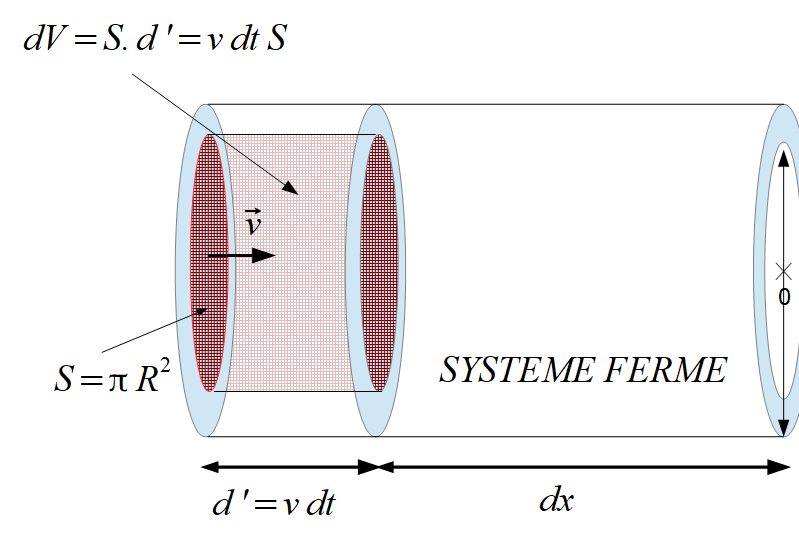
Ici, $dV = v dt S$
donc : $dH_l = \rho_l v dt S c_l dT$
Or le débit volumique $Q=v S$
$\Rightarrow$ $dH_l = \rho_l Q dt c_l dT$ $=\rho_l Q c_l \frac{dT}{dx} dx dt$
L’hypothèse d’équilibre thermodynamique entre l’eau liquide et la glace impose des variations liées de la température et de la pression de l’eau liquide en écoulement dans le canal. Compte tenu de cette hypothèse, on admet que la relation (2) prend la forme suivante :
$dH_l = c_l Q \frac{T(x)}{l_f} \frac{\rho_g – \rho_l}{\rho_g} \frac{dp}{dx} dx dt$ (3)
36.Röthlisberger estime dans son modèle que : $d𝐻_ℓ = \frac{1}{2} d𝐻_𝑔$. En déduire l’expression de la vitesse d’érosion $(\frac{d𝑅}{d𝑡})_{érosion}$ du canal en fonction de $𝑐_ℓ, 𝑄, 𝑅, ℓ_𝑓, 𝑇(𝑥), 𝜌_ℓ, 𝜌_𝑔 et \frac{d𝑝}{d𝑥} $.
$d𝐻_ℓ = \frac{1}{2} d𝐻_𝑔$ $\Rightarrow$ $c_l Q \frac{T(x)}{l_f} \frac{\rho_g – \rho_l}{\rho_g} \frac{dp}{dx} dx dt = \rho_g l_f \pi R dR dx$
$\Rightarrow$ $(\frac{d𝑅}{d𝑡})_{érosion} = \frac{c_l Q}{\pi R} \frac{T(x)}{l_f^2} \frac{\rho_g – \rho_l}{\rho_g^2} \frac{dp}{dx}$
37. Contrôler le signe de $(\frac{d𝑅}{d𝑡})_{érosion}$
Dans l’expression précédente, tous les paramètres sont positifs sauf $(\rho_g – \rho_l)$
Le signe de $(\frac{d𝑅}{d𝑡})_{érosion}$ dépend alors du signe de $\frac{dp}{dx}$ , l’énoncé nous indique que l’on peut remplacer $\frac{dp}{dx}$ par $−𝜌_𝑔 𝑔 sin 𝛼$ donc $\frac{dp}{dx}<0$ ce qui nous donne $(\frac{d𝑅}{d𝑡})_{érosion}>0$ soit un agrandissement des canaux.
En écrivant que l’érosion compense l’effet contraire de rétrécissement dû à la pression de la glace environnante, Röthlisberger obtient que le gradient de pression $\frac{d𝑝}{d𝑥}$ dans le canal de drainage varie inversement proportionnellement à son rayon $𝑅$.
On examine la situation de deux canaux parallèles voisins qui débouchent tous les deux au terminus du glacier où règne la pression atmosphérique. On suppose que l’un des canaux est caractérisé par un rayon supérieur à celui de l’autre canal.
38. En déduire comment se comparent les pressions dans les deux canaux à une même distance $𝐿$ de leur sortie.
On a : $\frac{dp}{dx} \simeq \frac{1}{R}$ si le rayon augmente alors le rapport $\frac{dp}{dx}$ diminue. La pression à l’entrée du canal le plus grand est plus petite que la pression à l’entrée de l’autre canal plus petit.
39. Expliquer pourquoi Röthlisberger conclut que le canal de plus grand diamètre absorbe le canal de moindre diamètre à l’occasion d’une connexion entre les deux canaux et qu’un réseau arborescent de drainage doit donc se développer à la base du glacier.
Nous venons de voir que la pression au sein de canaux de faibles rayons est grande. Or la forte pression participe à la fermeture des canaux. De plus dans les canaux plus larges, l’écoulement est facilitée (La résistance hydraulique est inversement proportionnelle au rayon) ce qui permet de dissiper plus d’énergie pour faire fondre les parois.
Les plus gros canaux absorbent les plus petits ce qui créé un réseau arborescent de drainage. En partant de multiples canaux étroits pour arriver à des canaux plus gros au fur et à mesure de la descente à l’image des cours d’eaux.
