Physique BCPST
G2E | 2023
Remarques générales
L’épreuve proposait, autour du thème des glaciers, une sélection de domaines du programme de physique de la prépa BCPST : mécanique des fluides, changement d’état, optique, mécanique et phénomènes de transfert.
L’épreuve était d’une difficulté contenue, elle proposait des raisonnements guidés assez proches du cours et des applications numériques ; les copies peu fournies sont rares et la plupart des questions ont été explorées par les candidats. Certains candidats semblent cependant avoir du mal à appréhender l’ensemble des informations données dans l’énoncé et ne comprennent pas (ou n’y prêtent pas assez attention) les schémas fournis (en optique en particulier). Le jury souhaite néanmoins signaler que des copies de très bonne qualité ont aussi été fournies et félicite les candidats à l’origine de telles copies.
On déplore en revanche un certain nombre de copies de présentation trop peu soignée : nombreuses ratures, pas de phrase explicative, questions traitées dans un ordre aléatoire (si des parties indépendantes peuvent être traitées dans un ordre quelconque, il est attendu que les questions d’une même partie soient abordées de façon connexe et consécutivement). De futurs ingénieurs doivent avoir le souci de l’expression écrite, indissociable de leur futur métier.
Le jury souhaite apporter les remarques suivantes sur le sujet 2023 ainsi que quelques recommandations :
• Il est important de vérifier l’unité des expressions fournies, une application numérique aberrante provient souvent d’une erreur faite en tout début de raisonnement : nous conseillons aux candidats de chercher à corriger de telles erreurs avant de poursuivre.
• Chaque réponse doit être justifiée avec soin.
– Par exemple dans la question 18, affirmer RN =mg ne suffit pas. Cette égalité, bien qu’étant valable ici, ne provient pas d’un équilibre du système mais d’un mouvement horizontal.
– Dans la question 30, le phénomène d’adhérence de la neige au contact du sol immobile implique U(0) nul. Dire que c’est parce qu’il n’y a plus de glace ou parce qu’on est au début de l’écoulement ou parce le fluide est newtonien est erroné.
Il est conseillé d’utiliser les unités usuelles comme les newtons N à la place de kg.m.s -2, les pascals Pa à la place de kgm -1.s-2
. En revanche dans la question 40, utiliser les unités de base est approprié puisqu’une analyse dimensionnelle est demandée.
• Les schémas demandés doivent être réalisés avec soin.
– Dans la question 6, les rayons doivent être distinguables des traits de construction. De plus, les lois doivent être données en cohérence avec les indications fournies sur le schéma (angles orientés ou non).
– Dans la question 8, un trajet précis du trajet du rayon est attendu : quelques calculs peuvent s’avérer nécessaires pour cela.
– Dans la question 42, il ne suffit pas de mettre certaines flèches, il faut également les légender et les représenter au bon endroit.
• Un schéma explicite et soigné avec quelques explications claires est préféré à de longues lignes de texte, l’explication y gagne en clarté et en rigueur :
– Ainsi, dans la question 9, relever sur le schéma les distances égales car des triangles sont isocèles permet de répondre rapidement à la question.
– Dans la question 17, un schéma soigné avec un bilan des forces (qui précise le nom des forces) permet d’aborder les questions suivantes avec rigueur. On rappelle à ce sujet que la réaction du support R est la somme vectorielle de la réaction normale R N et de la réaction tangentielle RT et que le schéma doit rendre compte de cela.
• Lire chaque partie dans son intégralité afin d’en saisir la logique apporte un recul nécessaire à toute résolution scientifique. Traiter dans l’ordre les questions de chaque partie ne peut qu’être utile à la démarche attendue.
– Ainsi dans la partie D, le théorème d’Euler est utilisé implicitement dans la question 26, et trouver la vitesse de l’écoulement demandé dans la question 24 fait appel à un autre raisonnement.
– Dans la partie E, tous les flux sont algébriques, comme précisé dans l’énoncé, les valeurs données dans la question 44 traduisent bien cela : certains flux ont une valeur positive et d’autres une valeur négative. Il ne faut donc pas ajouter un signe négatif devant les termes « sortants » ou « perdus » dans les bilans demandés dans les questions 36 et 43.
– Les problèmes et calculs mathématiques doivent être traités avec attention
– On voit par exemple des calculs de racine correspondant à un exposant non entier, certains contournent le problème en passant par ln et exp.
– La norme d’un vecteur ne semble pas toujours maitrisée (dans la majorité des copies, la norme est la somme des normes des composantes).
– On note une confusion de terme entre intégration et dérivation, de même qu’entre croissant et proportionnel.
– Beaucoup de candidats ne maitrisent pas le fonctionnement de leur calculatrice.
Des remarques plus spécifiques sur les différentes parties du sujet sont détaillées ci-dessous :
A. MATÉRIEL DE L’EXPÉDITION
Q1 : Il faudrait pour réaliser des applications numériques précises utiliser suffisamment de chiffres significatifs.
Q4 : On n’a pas ici un fluide incompressible, une surpression en ρg z ne peut être invoquée.
Q6 : Les lois de Snell-Descartes sont généralement connues mais rarement citées intégralement (notion de plan d’incidence souvent omise, jamais défini). Et si ces lois sont connues, elles ne sont généralement pas bien comprises : un rayon incident sous incidence normale (quand l’énoncé est compris !) donne lieu à deux rayons réfractés. On note aussi des erreurs dans les tracés des rayons (incohérents). Beaucoup de candidats ne semblent pas avoir compris que réflexion et réfraction ne sont pas exclusifs l’un de l’autre (exception faite de la réflexion totale) ce qui les conduit à faire deux schémas pour les lois de Snell-Descartes.
Rares enfin sont les candidats qui ont abordé avec succès la question sur la réflexion totale :
beaucoup de candidats l’envisagent à l’interface air-verre et obtiennent sans sourciller des résultats aberrants : n V = 1 ou 0.
B. SLALOM À SKI DANS UNE FORÊT
Le skieur est parfois assimilé à un ressort.
Q12 : Le vecteur d’onde k proposé a souvent des dimensions fantaisistes. Rappelons que comme toute fonction, cos (k x) possède un argument sans dimension.
C. FREINAGE D’UN TRAINEAU SUR LA GLACE
Il est important aussi de rappeler qu’un bilan de forces est différent d’une liste de vecteurs sans nom.
Q17 : Beaucoup d’étudiants ont imaginé une pente qui n’était pas présente dans l’énoncé.
Q18 : On suppose à peu près toujours un équilibre alors que RT = f RN n’est vrai que s’il y a glissement.
Q19 : Le théorème de Pythagore est non maitrisé et R=abs(RN +RT ) souvent proposé.
Q21 : Beaucoup de confusion sur les fonctions en python. Une grande tolérance a été accordée pour l’utilisation de odeint : V = odeint (derivee,v0,t) était attendu.
D. ÉCOULEMENT D’UN GLACIER
Q26 : Confusion fréquente entre cosinus et sinus dans la mise en œuvre de la projection.
Q28 : Trop de candidats se précipitent et parlent de fluide Newtonien. La notion de fluide newtonien n’est pas maîtrisée par beaucoup de candidats.
Q30 : L’adhérence du glacier sur la paroi rocheuse est rarement proposée. Confusion aussi entre conditions initiales et conditions aux limites.
E. BILAN THERMIQUE D’UN GLACIER
Les candidats n’ont pas toujours compris que les flux étaient définis comme surfaciques et algébriques. Beaucoup de candidats n’ont pas été attentifs à la convention utilisée. Il est précisé dans l’énoncé que « chaque flux est positif s’il est reçu par la surface, et négatif s’il est cédé par la surface ». Par exemple : LW out est donc négatif.
Sujet physique G2E 2023
Les glaciers du monde représentent environ 70% de la masse d’eau douce présente sur la planète sur une superficie de 15 millions de km2. La France quant à elle compte une surface glaciaire d’environ 300 km², répartie entre les massifs des Ecrins, de la Vanoise et du Mont-Blanc. Dans ce sujet, nous nous intéressons à des problèmes physiques liés aux glaciers. La partie A est consacrée au matériel de l’expédition (réchaud et jumelles). La partie B s’intéresse au slalom d’un skieur dans une forêt tandis que la partie C s’intéresse au temps de freinage d’un traîneau glissant sur la glace. La partie D traite de l’écoulement d’un glacier tandis que la partie E étudie les transferts thermiques au niveau du glacier. Les parties sont indépendantes.
A. MATÉRIEL DE L'EXPÉDITION
Évaluation de l’altitude par hypsométrie
Disposant d’un altimètre défectueux et mal étalonné, l’équipe scientifique souhaite évaluer son altitude h, en mesurant l’enthalpie de vaporisation de l’eau et en la corrélant à l’altitude (principe de l’hypsométrie).
Pour cela, on porte à ébullition de l’eau liquide de masse volumique $ \rho = 1,0.10^3 kg.m^{−3}$ grâce à un réchaud à gaz de puissance 𝑃 = 1230 W. Au bout d’une durée $ \Delta 𝑡 = 9,3 minutes $ après le début de l’ébullition, on constate que le niveau de l’eau dans une casserole cylindrique de diamètre 𝑑 = 15 cm, a diminué de $ \Delta 𝑥 =1,7 cm$.
1. Déterminer littéralement la masse $ \Delta m$ d’eau qui s’est vaporisée pendant la durée $\Delta 𝑡$. Faire l’application numérique pour $\Delta 𝑚$.
La masse d’eau vaporisée peut être retrouvée connaissant le volume d’eau vaporisée, en effet : $\Delta m = \rho V$ avec $V =S . \Delta x$ , soit :
$\Delta m = \rho \pi (\frac{d}{2})^2 \Delta x$
Application Numérique :
$\Delta m = 1,0.10^3 \pi (\frac{15.10^{-2}}{2})^2 . 1,7.10^{-2}$ $=0,3 kg$
2. Déterminer littéralement l’enthalpie massique de vaporisation 𝐿𝑣𝑎𝑝 de l’eau à l’altitude ℎ. Faire l’application numérique en exprimant 𝐿𝑣𝑎𝑝 en $J.g^{−1}$.
L’énergie de vaporisation $L_{vap}$ représente l’énergie nécessaire pour vaporiser 1g d’eau. Si on retrouve l’énergie totale utilisée pour vaporiser la masse $\Delta m$ alors on peut retrouver $L_{vap}$.
On connait la puissance du réchaud et son temps d’utilisation, donc l’énergie utilisée est de : $E_{vap} = P \times \Delta t$
Donc, $L_{vap}=\frac{P \Delta t}{\Delta m}$
Attention ici à bien convertir les minutes en secondes : $9,3 minutes$ $=9,3 \times 60 secondes$ , on laisse la masse en g car on veut $L_{vap}$ en $J.g^{-1}$
Application Numérique :
$L_{vap}=\frac{1230 \times 9,3 \times 60}{0,3}$ $=2,3.10^3 J.g^{-1}$
3. Déterminer numériquement, en °C, la température d’ébullition $\theta_{eb}$ de l’eau à l’altitude ℎ sachant qu’on a la relation empirique : $𝐿_{𝑣𝑎𝑝} = 𝐴 + 𝐵 \theta_{𝑒𝑏}$ avec $𝐴 = 2510 J.g^{−1}$, $𝐵 = − 2,54 J.g^{−1}.°C^{−1}$ et $\theta_{eb} en °C
La relation $𝐿_{𝑣𝑎𝑝} = 𝐴 + 𝐵 \theta_{𝑒𝑏}$ nous donne : $\theta_{𝑒𝑏} = \frac{L_{vap} -A}{B}$
Application Numérique :
$\theta_{𝑒𝑏} = \frac{2,3.10^3 – 2510}{-2,54}$ $=82,7°C$
4. Déterminer numériquement la pression 𝑃(ℎ) sachant que : log 𝑃sat = $5,1 - \frac{1660}{T_{eb}-45,7}$ avec $P_{sat}$ la pression de vapeur saturante en bar, log le logarithme à base 10 et $𝑇_{eb}$ la température d’ébullition en K.
log 𝑃sat = $5,1 – \frac{1660}{T_{eb}-45,7}$ donc $P_{sat} = $ $10^{(5,1 – \frac{1660}{T_{eb}-45,7})}$
Application Numérique :
$P_{sat} = $ $10^{(5,1 – \frac{1660}{(82,7+273,15) – 45,7})}$ $=0,56 bar $
5. La relation barométrique suivante permet enfin de déterminer ℎ connaissant 𝑃(ℎ) : $P(h) = P_0 (1 - \frac{0,0065h}{T_0})^{5,255}$ avec $P_0 = 1,013 bar$ et $T_0 = 288 K$ . Déterminer numériquement l’altitude ℎ de l’expédition.
$h = \frac{T_0}{0,0065}[1- \sqrt[5,255]{\frac{P(h)}{P_0}}]$
Application Numérique :
$h=4734m$
Jumelles à prismes
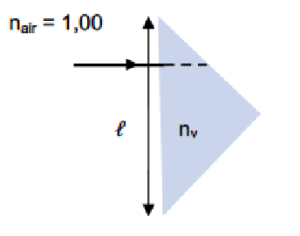
On utilise pour les observations une jumelle qui contient un objectif, un dispositif redresseur à base de prismes et un oculaire. On commence par étudier le trajet de la lumière à travers un prisme rectangle isocèle, en verre d’indice $𝑛_v$ = 1,50. Pour des raisons de clarté, le prisme est représenté en coupe dans le plan d’incidence. On s’intéresse à un rayon lumineux arrivant sur la normale du prisme comme indiqué sur la figure ci-dessous :
6. Rappeler les lois de la réflexion et les lois de la réfraction de Snell-Descartes en vous appuyant sur un schéma.
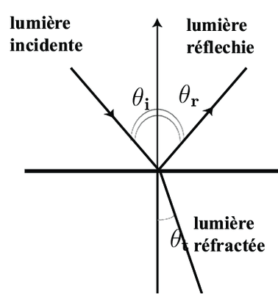Soit un rayon en incidence quelconque sur un dioptre séparant 2 milieux d’indice différents ($n_1$ et $n_2$). Ici nous ne donnons pas de sens aux angles.
Le rayon réfléchi, le rayon réfracté, le rayon incident et la normale (au dioptre) sont contenus dans le plan d’incidence.
Loi de la réflexion :
les angles incidents et réfléchis sont égaux $\theta_i = \theta_r$
Loi de la réfraction :
La relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incident θi et réfracté θt, appelée relation de Snell-Descartes, s’écrit :
$n_1 sin(\theta_i) = n_2 sin(\theta_t)$
7. L’indice de l’air extérieur dans lequel baigne le prisme est égal à 1,00. Calculer la valeur limite de l’indice du prisme noté $n_{V,lim}$ assurant la réflexion totale à l’interface verre-air
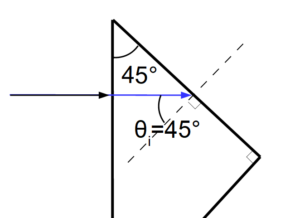
Le rayon dans le prisme atteint l’interface prisme/air avec un angle incident de 45°. Pour connaitre la valeur de l’indice minimale du prisme il faut considérer que l’angle réfracté a atteint la valeur de 90°. On obtient la relation :
$n_{V,lim} sin(\theta_i) = n_{air} sin(\theta_r)$, soit $n_{V,lim} = \frac{n_{air} sin(\theta_r)}{sin(\theta_i)}$
Application Numérique :
$n_{V,lim} = \frac{1 \times sin(90)}{sin(45)}$ $=1,41$
8. Représenter sur votre copie le trajet d’un rayon lumineux qui, une fois entré dans le prisme, est réfléchi sur les deux faces du prisme. Préciser la direction du rayon sortant du prisme.
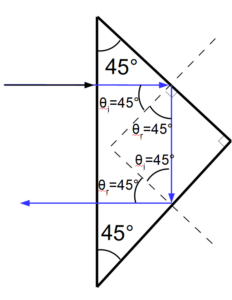
Les angles incidents et réfléchis sont tous égaux à 45° par conséquent le rayon revient parallèle au rayon incident.
9. Par des considérations géométriques, montrer que la distance parcourue dans le prisme par le rayon lumineux vaut ℓ, longueur de l’hypoténuse.
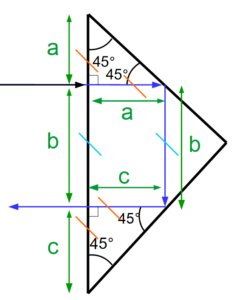
Ici $a+b+c = l$ (hypothénuse) or en haut et en bas on retrouve 2 triangles rectangles isocèles donc les chemins horizontaux du rayon correspond aux cotés a et c. (Ils sont d’ailleurs égaux entre eux : a = c)
Enfin les rayons dans le prisme ainsi que le coté b du prisme forment un rectangle, donc les cotés b sont égaux.
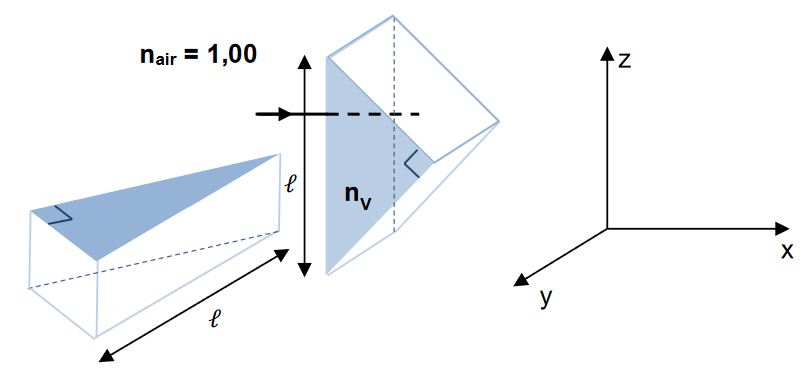
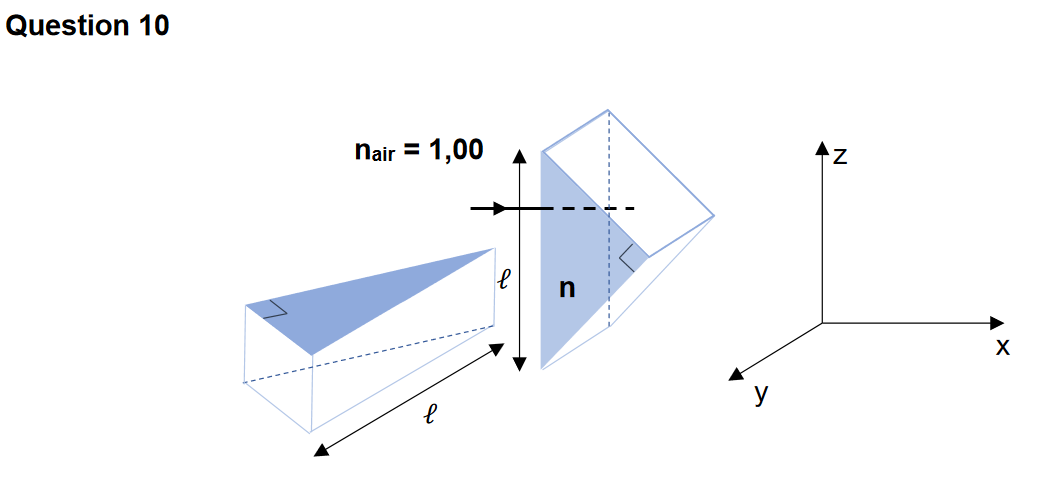
On s’intéresse maintenant au dispositif redresseur complet mettant en œuvre 2 prismes isocèles rectangles dont les hypoténuses sont perpendiculaires entre elles et à la direction initiale du faisceau incident. Le faisceau incident se propage suivant l’axe 𝑥. L’hypoténuse du premier prisme est orientée suivant 𝑧 et celle du second prisme suivant 𝑦.
10. Représenter sur l'annexe à joindre avec la copie, le trajet d’un rayon lumineux qui rentre dans le redresseur. Préciser la direction du rayon sortant du dispositif.
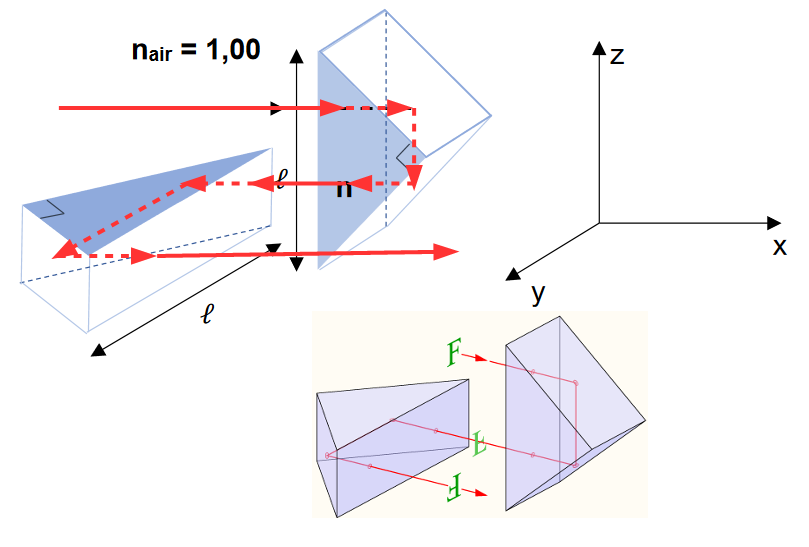
Le rayon sortant est parallèle au rayon entrant.
11. Outre son caractère redresseur, le dispositif précédent permet un gain de chemin optique, ce dernier étant défini comme le produit de l’indice du milieu par la distance parcourue. Evaluer le gain en chemin optique noté $\Delta$ apporté par le dispositif à prismes en supposant les prismes accolés.
A la question 9 nous avons démontré que le chemin du rayon dans le prisme est égal à $l$ (hypoténuse du prisme). Dans le redresseur, le rayon traverse 2 prismes identiques, le rayon parcours alors une distance 2$l$.
Le gain, défini comme le produit de l’indice du milieu par la distance parcourue est égal à : $\Delta = n_v \times 2 \times l$
B. SLALOM A SKI DANS UNE FORET
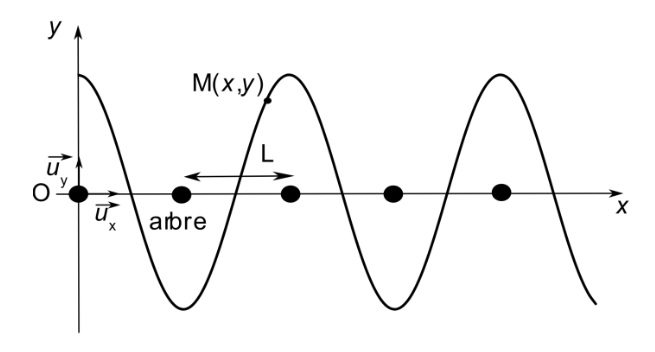
Afin de rejoindre le glacier, l’équipe scientifique traverse à ski une forêt. Un skieur, assimilé à un point matériel M, réalise un slalom dans une forêt où les arbres sont supposés régulièrement espacés d’une distance 𝐿 = 100 m suivant l’axe 𝑂𝑥 de la pente (voir figure ci-dessous). On note 𝑂𝑦 la direction horizontale perpendiculaire à la pente (𝑂𝑥). A 𝑡 = 0, le skieur se trouve en $M_0$ (0, $y_0$). On suppose que le skieur suit une trajectoire sinusoïdale $𝑦(𝑥) = 𝑦_0 . cos(𝑘𝑥)$ et qu’il conserve à tout moment une vitesse dont la composante suivant 𝑂𝑥 est constante : $𝑥̇ = 𝑣_0 = 30 km.h^{−1}$. On s’intéresse ici à l’étude cinématique du mouvement du skieur, décrivant une trajectoire sinusoïdale :
12.Exprimer 𝑘 en fonction de 𝐿.
Pour la position en y(t), on retrouve la périodicité du cosinus tous les 2 $\pi$ lorsque l’on atteint une distance de 2L , $cos(kx) = cos(kx +2 \pi )$
Ici, $cos(0) =cos(2 \pi) = cos(k 2L )$,
soit : $k2L=2\pi $ ce qui nous donne $k = \frac{\pi}{L}$
$y(x)=y_0 cos(\frac{\pi x}{L})$
13.Exprimer 𝑥(𝑡) puis 𝑦(𝑡)
$x(t) = v_0 t + x_0$ $= v_0 t$
on remplace x dans y(x)
$y(t) = y_0 cos(\frac{\pi v_0 t}{L})$
14.En déduire l’expression de la période temporelle 𝑇 des oscillations du skieur en fonction de 𝐿 et de $𝑣_0$. Faire l’application numérique sur 𝑇.
On peut réecrire $y(t) = y_0 cos(\omega t )$ avec $\omega$ la pulsation, ici $\omega = \frac{2 \pi}{T}$.
$\frac{2 \pi}{T} = \frac{\pi v_0}{L}$ \rightarrow$ $T=\frac{2L}{v_0}$
Application Numérique :
$T = \frac{2 \times 100}{\frac{30}{3.6}}$ $=24s$
15. Donner les expressions des vecteurs vitesse $\vec{v}$ et accélération $\vec{a}$ du skieur sur la base cartésienne ($\vec{u_x}, \vec{u_y}$).
Vecteur vitesse :
$\vec{v} = v_0 \vec{u_x} + \dot{y}(t) \vec{u_y}$ $=v_0 \vec{u_x} – y_0 \frac{\pi v_0}{L}sin(\frac{\pi v_0 t}{L}) \vec{u_y}$
Vecteur accélération :
$\vec{a} = 0 . \vec{u_x} – y_0 (\frac{\pi v_0}{L})^2 cos(\frac{\pi v_0 t}{L}) \vec{u_y}$
16. Pour que le skieur reste debout, il doit avoir une accélération inférieure à $0,7𝑔$ où $𝑔 = 9,8 m.s^{−2}$ est l’accélération de la pesanteur. Quelle est alors l’amplitude maximale $𝑦_{0,max}$ que peut adopter le skieur sans chuter ? Faire l’application numérique sur $𝑦_{0,max}$.
On a l’accélération maximale pour $cos(\frac{\pi v_0 t}{L})=1$ $\rightarrow$ $-y_0 (\frac{\pi v_0}{L})^2 \lt a_{max}= 0.7g$
$y_{0,max} = \frac{0.7 g L^2}{(\pi v_0)^2}$
Application Numérique :
$y_{0,max} = \frac{0.7 \times 9,8 \times 100^2}{(\pi \frac{30}{3,6})^2}$ $=100m$
C. FREINAGE D'UN TRAINEAU SUR LA GLACE
On s’intéresse ici au freinage sur la glace d’un traineau portant l’équipement et les instruments de mesure de l’expédition, la masse totale vaut 𝑚 = 80 𝑘𝑔 : à 𝑡 = 0, le traineau se trouve en O, origine du repère et se déplace horizontalement suivant l’axe x, l’axe z désignant l’axe vertical. Sa vitesse initiale vaut $𝑣_0 = 20 km.h^{−1}$ et il se déplace dans le sens de 𝑥 croissant. Il est alors soumis à une réaction $\vec{R}$ de la part de la glace et à une force de frottement $\vec{F}=-m \alpha v^2 \vec{u_x}$ de la part de l’air, où 𝑣 est la norme du vecteur vitesse et $\alpha$ une constante positive. On suppose que les lois de Coulomb du frottement solide s’appliquent de telle sorte que $𝑅_𝑇 = 𝑓𝑅_𝑁$ avec 𝑓, coefficient de frottement solide, $𝑅_𝑇$ et $𝑅_𝑁$ étant respectivement les valeurs absolues des composantes tangentielles et normales de la réaction $\vec{R}$. On cherche à déterminer le temps $𝑡_a$ mis par le traineau pour s’arrêter. On donne 𝑚 = 80 kg ; 𝑓 = 0,20 ; $𝑔 = 9,8 m.s^{-2}$ et $\alpha = 0,1 SI$.
17. Faire un bilan des forces s’exerçant sur le skieur et les représenter sur un schéma.
Bilan des forces :
Le poids : $\vec P$ ; La force de frottement de l’air $\vec F$ ; La force de réaction $\vec R$ décomposée en force de réaction normale $\vec R_N$ et la force de réaction tangentielle $\vec R_T$ soit $\vec R = \vec R_N + \vec R_T$
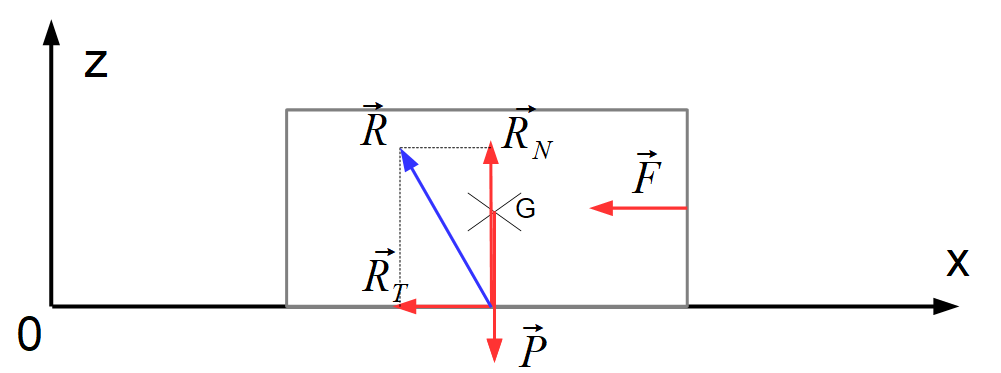
18. Exprimer $𝑅_𝑁$ et $𝑅_𝑇$ en fonction de 𝑚, 𝑔 et 𝑓. Faire les applications numériques.
On applique la deuxième loi de Newton :
$\sum \vec F = m \vec a$
Si on projète sur l’axe (Oy) on obtient :
$R_N – P = m a_y =0$ ( $a_y=0$ car il n’y a pas de déplacements selon y)
$\rightarrow R_N=P=mg $
Application Numérique :
$ R_N= 80 \times 9,8 = 784N $
Il vient : $R_T = f R_N = fmg$
Application Numérique :
$R_T = 0,2 \times 80 \times 9,8 = 156,8N$
19. Exprimer 𝑅, la norme de $\vec R$ puis calculer sa valeur numérique.
$R = \sqrt{R_N^2 + R_T^2}$
Application Numérique :
$R = \sqrt{784^2 + 156,8^2} =800N$
20. Montrer que l’équation différentielle du mouvement peut se mettre sous la forme : $\frac{dv}{dt} = - \beta - \alpha v^2$. On exprimera $\beta$ en fonction de 𝑔 et 𝑓.
On projète le PFD sur l’axe (Ox) :
$-F – R_T = m a_x$
$-m \alpha v^2 – fmg = m a_x$
$a_x = \frac{dv}{dt} = -fg -\alpha v^2$
Par identification : $\beta = fg$
On donne ci-dessous un programme Python utilisant l’outil odeint du module scipy.integrate et permettant de résoudre numériquement l’équation différentielle précédente.
1 from scipy.integrate import odeint
2 import numpy as np
3 import matplotlib.pyplot as plt
4 g=9.8
5 alpha=0.10
6 f=0.2
7 beta= # à compléter
8 # Définition de l’équation différentielle
9 def derivee(v, t):
10 return -beta-alpha*v*v
11 t0 = 0
12 tf = 3 # seconde
13 v0 = # à compléter
14 t = np.linspace(t0, tf, 1000)
15 # Résolution
16 v = # à compléter
17 # tracés
18 plt.plot(t, v[:, 0], ‘b—’)
19 plt.ylabel(‘vitesse (m/s)’)
20 plt.xlabel(« Temps (s) »)
21 plt.grid()
22 plt.legend()
23 plt.show()
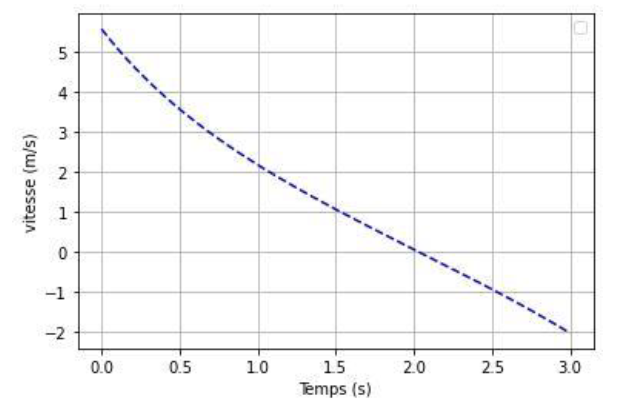
On obtient le graphe ci-dessous, représentant l’évolution temporelle de la vitesse :
21. Recopier et compléter les lignes 7, 13 et 16 du programme.
7. beta = f * g
13. v0 = 20/3,6
(attention au passage $km.h^{-1}$ en $m.s^{-1}$)
16. v = odeint(derivee,v0,t)
22. A partir du graphe ci-dessus, déterminer numériquement le temps d’arrêt $𝑡_a$ du mobile.
La vitesse devient nulle pour t=2s.
D. ÉCOULEMENT D'UN GLACIER
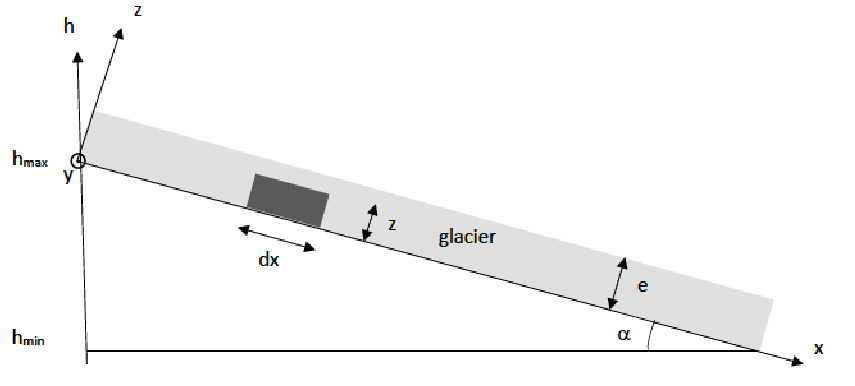
On s’intéresse à l’écoulement du glacier des Bossons dans la vallée de Chamonix : l’altitude maximale du glacier est $ℎ_{max} = 4700 m$ et son altitude minimale $ℎ_{min} =1400 m$. La pente moyenne du glacier, supposée constante, fait un angle $\alpha = 28° $ avec l’horizontale ; son épaisseur supposée constante est 𝑒 = 120 m et sa largeur supposée constante est 𝐿 = 1200 m (suivant la direction (𝑂𝑦) perpendiculaire au schéma). On adopte le système d’axes représenté ci-dessous : (𝑂𝑥) est dirigé suivant la pente du glacier et (𝑂𝑧) dirigé suivant la hauteur du glacier. On donne : la masse volumique de la glace $\rho_{glace} = 920 kg.m^{−3}$ ; la viscosité dynamique de la glace considérée comme un fluide newtonien $\eta_{glace} =1,0.10^{10} Pa.s $; l’accélération de la pesanteur $𝑔 = 9,8 m.s^{−2}$.
En 1966 a eu lieu le crash d’un Boeing 707 d’Air India au sommet du glacier. Parmi la cargaison, des pierres précieuses ont été retrouvées au bas du glacier en 2013 par un randonneur chanceux.
Régime d’écoulement du glacier
23. Exprimer littéralement puis calculer numériquement en tonnes, la masse $𝑚_{glace}$ du glacier.
La masse du glacier $m =\rho \times V$ avec V : volume du glacier = $e\times L \times l$, ici $l$ représente la longueur de la pente (soit l’hypoténuse du triangle).
On retrouve $sin \alpha = \frac{(h_{max} – h_{min})}{l}$ , soit $l=\frac{(h_{max} – h_{min})}{sin \alpha} $
On retrouve une masse $m= \frac{\rho \times e \times L \times (h_{max}- h_{min})}{sin \alpha}$
Application Numérique :
$m= \frac{920 \times 120 \times 120 \times (4700- 1400)}{sin 28}$ $=9,3.10^{11} kg$ $=9,3.10^8 tonnes$
24. A l’aide des données, exprimer littéralement puis calculer numériquement la vitesse d’écoulement 𝑈 du glacier.
On peut utiliser l’information donnée après le schéma. Les pierres précieuses ont parcourues la distance $l$ en 47ans. Elles avancent à la même vitesse que le glacier.
Soit $U = \frac{d}{\Delta t}$ $=\frac{h_{max}-h_{min}}{sin \alpha \times \Delta t}$
Application Numérique :
$U =\frac{4700 -1400}{sin 28 \times 47}$ $=149,6 m.an^{-1}$ $=4,74.10^{-6} m.s^{-1}$
25. Définir puis calculer le nombre de Reynolds 𝑅e associé à l’écoulement du glacier. Conclure sur la nature de l’écoulement.
Nombre de Reynolds : $R_e = \frac{U \times L}{\nu}$ $=\frac{\rho \times U \times L}{\eta}$
Application Numérique :
$R_e =\frac{920 \times 4,74.10^{-6} \times 1200}{1,0.10^{10} }$ $=5,25.10^{-10}$
C’est un écoulement rampant.
Profil des vitesses dans une section droite du glacier
On s’intéresse à l’écoulement d’une particule fluide de hauteur 𝑧 et de surface d𝑆 = 𝐿d𝑥, et représentée sur la figure précédente.
On suppose que le glacier s’écoule sous l’effet de son poids en régime permanent, de telle sorte que la force de viscosité $d𝐹 = 𝜏_T d𝑆$ est compensée par la composante tangentielle du poids.
26. Exprimer la contrainte tangentielle visqueuse $𝜏_T(𝑧)$ en fonction de $\rho_{glace}$, 𝑔, 𝑧 et $\alpha$.
Sur le schéma on peut placer $\vec dF$ et le poids décomposé en sa composante tangentielle et sa composante normale.
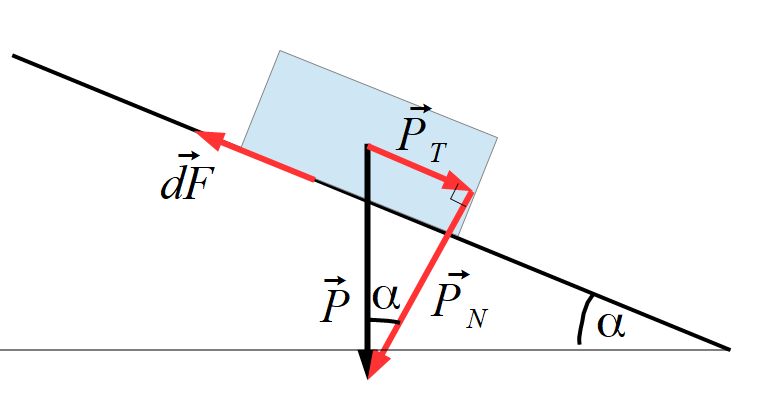
L’énoncé nous donne l’égalité entre la force de viscosité dF et la composante tangentielle du poids $P_T$
$dF=P_T $ $\rightarrow$ $ \tau _T dS = P sin \alpha = mg sin \alpha$ $=\rho_{glace} V g sin \alpha$ $=\rho_{glace} z dS g sin \alpha$ soit :
$\tau _T = \rho_{glace} z g sin \alpha$
27. En déduire l’expression de $𝜏_T(𝑒)$ puis faire l’application numérique. Comparer la valeur obtenue à la pression atmosphérique.
$\tau_T(e) = \rho_{glace} g e sin \alpha$
Application Numérique :
$\tau_T(e) = 920 \times 9,8 \times 120 \times sin (28)$ $=5,08.10^5 Pa$
On retrouve $\tau_T(e) \simeq 5 \times P_{atm}$
On suppose que la relation entre le gradient des vitesses (ou taux de cisaillement) $\dot \gamma = \frac{dU}{dz}$ et la contrainte tangentielle visqueuse $𝜏_T(𝑧)$ suit la loi de Glen : $\dot \gamma = \frac{dU}{dz} = 𝐴(𝑇) \tau_𝑇 ^3 $ avec 𝐴(𝑇) un facteur dépendant de la température 𝑇 selon la loi : $𝐴(𝑇) = 𝐴_0 e^{− \frac{Q}{RT}}$ où 𝑄 désigne l’énergie d’activation (en $J.mol^{−1}$) associée au phénomène et 𝑅 la constante des gaz parfaits. On se placera à une température égale à 𝜃 = −10 °𝐶 .
28. La glace peut-elle être considérée comme un fluide visqueux newtonien ? Justifier.
Un fluide Newtonien est un fluide dont la loi $contrainte-vitesse de déformation$ doit être linéaire, ce n’est pas le cas ici, le glacier est donc un fluide visqueux non Newtonien.
29. On qualifie la relation 𝐴(𝑇) d’arrhénienne. Justifier ce qualificatif et donner l’influence de la température sur l’écoulement.
A(T) est une relation arrhénienne car elle dépend de la température en $A e^{1/T}$ équivalent à la loi d’Arrhénius : $k=A e^{- \frac{E_a}{RT}}$.
Ici si T augmente alors A(T) augmente (évolution en $e^{-x}$ avec x décroissant) .
30. On cherche à déterminer le profil des vitesses 𝑈(𝑧). Justifier que 𝑈(0) = 0.
U(0) correspond à la vitesse de la couche directement en contact avec le sol. La couche de fluide visqueux directement en contact avec la paroi à la vitesse de la paroi. Ici le sol est immobile donc U(0)=0.
31. Intégrer, par séparation des variables, la loi de Glen pour en déduire le profil des vitesses 𝑈(𝑧).
Loi de Glen : $\frac{dU}{dz} = 𝐴(𝑇) \tau_𝑇 ^3 $
Séparation des variables :$dU = 𝐴(𝑇) (\rho_{glace} . z . g . sin\alpha)^3 dz$
Intégration :
$ \int_{U(0)}^{U(z)} dU = \int_{0}^{z} 𝐴(𝑇) (\rho_{glace} . g . sin\alpha)^3. z^3 . dz$ $\Rightarrow$ $U(z) – U(0) = A(T) (\rho_{glace} . g . sin \alpha)^3 [\frac{z^4}{4}]_0^z$
$U(z) = \frac{A(T) (\rho_{glace} .g.sin \alpha)^3 . z^4}{4} $
32. En déduire 𝑈(𝑒) et faire l’application numérique. On donne : $𝐴 = 10^{−24}$ pour 𝜃 = −10 °𝐶. Comparer au résultat de la question 24.
$U(e) = \frac{A(T) (\rho_{glace} .g.sin \alpha)^3 . e^4}{4} $
Application Numérique :
$U(e) = \frac{10^{-24} (920 \times 9,8 \times sin (28))^3 . 120^4}{4} $ $=3,9.10^{-6} m.s^{-1}$
Le résultat est proche de celui de la question 24 ($4,76.10^{-6}m.s^{-1}$)
E. BILAN THERMIQUE D'UN GLACIER
Les glaciers, de par leur faible inertie de réponse aux changements climatiques, sont des outils de choix pour comprendre l’augmentation globale de température observée depuis le XIXème siècle. La relation entre l’évolution des glaciers et la variabilité climatique repose en partie sur une étude du bilan d’énergie de surface du glacier. Pour effectuer ce bilan, on considère le volume compris entre la surface et une profondeur à partir de laquelle il n’existe plus de flux radiatifs significatifs comme l’indique la figure ci-dessous.
Nous allons effectuer un bilan en termes de flux surfacique pour déterminer l’énergie stockée par unité de surface et par unité de temps, du volume étudié, que l’on notera Φ ; cette dernière a pour effet d’augmenter ou de diminuer la température de la glace et peut également induire la fonte de la glace ou la solidification de l’eau liquide.
Le bilan fait apparaître les flux suivants (chaque flux est positif s’il est reçu par la surface, et négatif s’il est cédé par la surface) :
• Des flux surfaciques radiatifs arrivant « in » et partant « out » de la surface notés $𝑆𝑊_{in}$ et $𝑆𝑊_{out}$ pour les radiations de courtes longueurs d’onde (Short Waves de longueur d’onde comprise entre 0,15 et 3 μ𝑚) et $𝐿𝑊_{in}$ et $𝐿𝑊_{out}$ (Long Waves) pour les radiations de grandes longueurs d’onde (de 3 à 100 μ𝑚) ;
• Des flux surfaciques de convection : 𝐿𝐸 le flux turbulent de chaleur latente (permet à la neige de se sublimer une fois au sol ; il dépend de la vitesse du vent, de l’humidité mais aussi de la densité de l’air et de la chaleur latente de sublimation) et 𝐻 le flux turbulent sensible (permet à la neige déposée de changer de température ; il dépend de la densité de l’air, de la capacité thermique massique à pression constante de l’air mais aussi de la vitesse du vent et de la température de la neige) ;
• Du flux surfacique 𝑃 induit par les précipitations ;
• Du flux surfacique conductif 𝐺 dans la neige/glace.
On ne s’intéresse qu’à des flux verticaux par rapport au volume de glace étudié, supposé horizontal et on se place en géométrie axiale d’axe 𝑂𝑧. Aucune connaissance spécifique sur le transfert thermique par rayonnement n’est nécessaire pour traiter cette partie.
Un corps noir de température absolue 𝑇 émet un rayonnement thermique. La loi de Wien donne la longueur d’onde pour laquelle l’émittance (puissance émise par unité de surface du corps noir et par unité de longueur d’onde) est maximale à la température 𝑇 du corps noir :
$𝜆_{max} = \frac{𝑐𝑡𝑒}{𝑇}$ avec $𝑐𝑡𝑒 = 2,898. 10^{−3} m.K$.
La loi de Stefan-Boltzmann donne l’expression de la puissance surfacique rayonnée (émittance énergétique totale, prenant en compte toutes les longueurs d’onde) :
$𝜙_{𝑡ℎ}(𝑇) = 𝜎𝑇^4$
$𝜎 = 5,67. 10^{−8} W.m^{-2}.K^{-4}$ est la constante de Stefan-Boltzmann.
33. Qu’est-ce-qui distingue les transferts thermiques par conduction ou convection des transferts thermiques par rayonnement ? Qu’est-ce-qui distingue les transferts thermiques par conduction des transferts thermiques par convection ?
-Les transferts thermiques par conduction ou convection ont besoin d’un support pour se propager contrairement au rayonnement qui peut se propager dans le vide.
-Dans les transferts thermiques par conduction, il n’y a pas de déplacement de la matière, le déplacement se fait de proche en proche.
34. Justifier, par un calcul de longueur d’onde en μ𝑚, que les radiations courtes longueurs d’onde sont dues au Soleil (température moyenne $𝑇_S = 5778 K$) alors que les radiations grandes longueurs d’onde sont dues au système terrestre (température moyenne $𝑇_T = 300 K$).
On calcul $\lambda_{max}$ pour le Soleil et la Terre :
$\lambda_{max,Soleil} = \frac{cte}{T}$ $=\frac{2,898.10^{-3}}{5778}$ $=0,5µm$ (ordre de grandeur des courtes longueurs d’ondes)
$\lambda_{max,Terre} = \frac{cte}{T}$ $=\frac{2,898.10^{-3}}{300}$ $=9,7µm$ (ordre de grandeur des grandes longueurs d’ondes)
35. Calculer le flux radiatif $𝐿𝑊_{out}$ dans le cas où la neige/glace se comporte comme un corps noir de température égale à −2,6°C.
$LW_{out} = \sigma T^4$ , le signe sera négatif car l’énergie est cédé par la surface.
Application Numérique :
$LW_{out} = -5,67.10^{-8} . (273-2.6)^4$ $= -303 W.m^{-1}$
36. On note 𝑅 le flux radiatif global. Exprimer 𝑅 en fonction de $𝑆𝑊_{in}, 𝑆𝑊_{out}, 𝐿𝑊_{in} et 𝐿𝑊_{out}$.
$R = SW_{in} + SW_{out} + LW_{in} + LW_{out}$
R représente la somme des flux. La valeur de chaque flux aura un signe positif ou négatif en fonction de l’énergie cédée ou reçue.
37. Le flux diffusif 𝐺 suit la loi de Fourier. Donner l’expression de 𝐺 dans ce contexte en précisant les unités et la signification physique des différents termes.
$G = \frac{P_{th}}{S} = – \lambda \frac{dT}{dz}$
Avec G: Le flux surfacique (en $W.m^{-2}$). Représente le flux de chaleur qui passe à travers une surface de contrôle.
$\lambda$ : conductivité thermique (en $W.m^{-1}.K^{-1}$). Grandeur intrinsèque au matériau qui caractérise la capacité de diffuser la chaleur.
$d T$ : Variation de température (en Kelvin : K). Représente la variation de température entre 2 surfaces de contrôles. La variation de la température est la cause qui permet le déplacement du flux de chaleur.
dz : Longueur caractéristique (en mètre : m) entre les 2 surfaces de contrôles.
38. Que vaut 𝐺 dans le cas d’un glacier isotherme ?
Si le glacier est isotherme, on a dT =0 soit un flux surfacique G = 0.
39. Le flux surfacique apporté par les précipitations suit une loi de type loi de Newton : donner l’expression de 𝑃 en fonction du coefficient de transfert thermique ℎ, de la température de la neige qui tombe $𝑇_n$ et de la température de la surface du glacier $𝑇_{surf}$ dans le cas$ 𝑇_n > 𝑇_{surf}$.
On a $T_n > T_{surf}$, ce qui implique un flux de chaleur de la neige vers le glacier (le flux de chaleur se dirige toujours de la température la plus élevé vers la température la moins élevée). Le glacier reçoit donc de la chaleur, le flux surfacique P doit être positif.
$P = \frac{\Phi}{S} = h \Delta T$ $=h (T_n – T_{surf})$
Le coefficient ℎ dépend de la masse volumique de la neige 𝜌, de sa capacité thermique massique $𝑐_n$ et de l’intensité 𝐼 de précipitation : $ℎ = 𝜌^a 𝑐_n^b 𝐼^c$.
Par la suite, on prendra $𝜌 = 0,20 kg.L^{−1}$, $𝑐_n =2090 J.K^{−1}.kg^{−1}$ et $𝐼 =2,0 mm.heure^{−1}$.
40. Par analyse dimensionnelle, déterminer a, b et c et exprimer ℎ en fonction de 𝜌, $𝑐_n$ et 𝐼
L’unité de h est en $W.m^{-2}.K^{-1}$
Si on analyse $[\rho] \times [c_n] \times [I]$, on retrouve : $\frac{M}{L^3} \times \frac{J}{K . M} \times \frac{L}{T}$ $=\frac{J}{L^2 . K . T}$ soit $J.m^{-2}.K^{-1}.s^{-1}$, or le $J.s^{-1}=W$ ce qui donne une unité en $W.m^{-2}.K^{-1}$ ce qui correspond à l’unité de h.
On retrouve alors $a=b=c=1$ soit : $h= \rho c_n I$
41. Faire l’application numérique sur 𝑃 lorsque la différence de température entre la neige qui tombe et la surface du glacier vaut 5 °𝐶.
$P=h \Delta T$ $=\rho . c_n.I. \Delta T$
(attention aux unités!)
Application Numérique :
$P= 0,20.10^3 \times 2090 \times (\frac{2.10^{-3}}{3600}) \times (5)$ $=1,16W.m^{-2}$
42. Compléter sur l'annexe, le schéma en indiquant les flux énergétiques et en précisant leur sens par une simple flèche (voire une double flèche si le sens du flux n’est a priori pas connu).
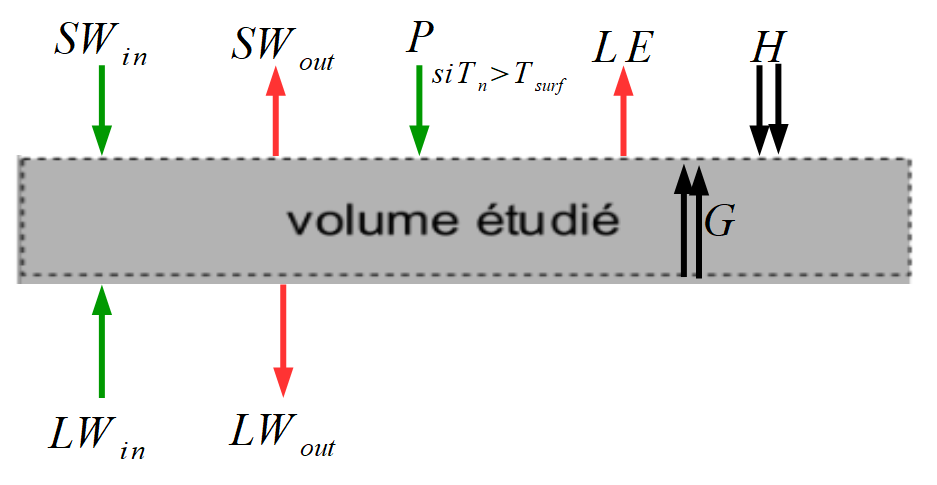
Les flux radiatifs SW et LW sont positifs si ils sont entrants et négatifs si ils sont sortants.
Le flux P est positif si $T_n>T_{surf}$, (ce qui est le cas ici) négatif sinon.
Le flux LE permet à la neige de se sublimer et a donc besoin de l’énergie de la surface, donc c’est un flux sortant.
Le flux H dépend de la température de la neige et de la surface ainsi que d’autres paramètres non accessible donc le sens n’est pas défini.
Le flux G dépend des températures de la surface supérieure et inférieure. Paramètres non donnés donc le sens ne peut être défini.
43. A l’aide d’un bilan thermique, exprimer l’énergie stockée Φ par unité de surface et unité de temps en fonction des flux surfaciques 𝑅, 𝐿𝐸, 𝐺, 𝐻 et 𝑃.
$\Phi = R + LE + G + H+ P$
44. Calculer Φ lorsque $𝑅 =15,8 W.m^{−2}$, $𝐿𝐸 = −18,1 W.m^{−2}$ et $𝐻 = 6,1 W.m^{−2}$.
Application Numérique :
$\Phi = 15,8 – 18,1 + 0 +6,1+ 1,16$ $=4,96W.m^{-2}$
45. En raisonnant sur le signe de l’énergie stockée, expliquer en respectant l’ordre chronologique les phénomènes ayant lieu dans la neige/glace.
On retrouve une énergie positive donc une énergie reçu par le glacier qui aura comme conséquence une élévation de sa température.
Par ordre chronologique (ceci est une suggestion de réponse) :
On a tout d’abord le flux $SW_{in}$ du Soleil puis par réflexion $SW_{out}$. Vient également les flux $LW_{in} et LW_{out}$ issus de la Terre.
Dans l’atmosphère ces flux peuvent créer des précipitations (flux P) qui une fois au sol créées un flux H et/ou LE.
Enfin le flux G existera si il y a une différence de température sur la face supérieure et inférieure de la glace.
8 réponses
lors de la question 41 , je subodore une erreur . L’énoncé suggère une élévation de température de 5°C . Or dans la loi de Newton , il s’agit de delta T donc une variation soit 5 K ou 5 °C et pas 273 +5 !!!!!!!
Ai-je raison ?????
Oui vous avez raison, merci à vous. J’ai mis à jour la correction.