Physique BCPST
G2E | 2024
ÉPREUVE ÉCRITE DE PHYSIQUE
Des copies de qualité ont été fournies et le jury félicite les candidats à l’origine de telles copies. Une partie non négligeable des candidats ont abordé une grande partie des questions. La présentation des copies, le soin apporté à la rédaction, l’orthographe et le fait que les résultats soient encadrés ou soulignés ont été pris en compte dans le barème pour 1 point sur 20.
Remarques générales
Le jury apporte les remarques suivantes sur le sujet 2024 ainsi que quelques recommandations.
• Il est important de vérifier l’unité des expressions fournies, une application numérique aberrante provient souvent d’une erreur faite en tout début de raisonnement : nous conseillons aux candidats de chercher à corriger de telles erreurs avant de poursuivre. Sauf pour les grandeurs sans dimension, une application numérique doit conduire à une valeur numérique suivie d’une unité.
• Chaque réponse doit être justifiée avec soin. Par exemple, à la question 13, le fait qu’une transformation adiabatique réversible puisse être considérée comme isentropique doit être justifié à partir de l’écriture du second principe de la thermodynamique.
• Les candidats doivent s’assurer d’avoir une rédaction précise et un langage correct : ainsi en est-il par exemple des questions 20 et 22 où le terme « gradient de concentration » permet de justifier l’apparition d’un flux diffusif.
• Il est conseillé d’utiliser les unités usuelles comme les joules J à la place de $kg.m^2 .s^{-2}$ (question 3), les pascals Pa à la place de $kgm^{-1}.s^{-2}$ (question 37). En revanche dans la question 28, utiliser les unités de base est approprié puisqu’une analyse dimensionnelle est demandée.
• Les schémas demandés doivent être réalisés avec soin, par exemple à la question 44 pour illustrer les lois de la réflexion et de la réfraction.
• Lire chaque partie dans son intégralité afin d’en saisir la logique apporte un recul nécessaire à toute résolution scientifique. Traiter dans l’ordre les questions de chaque partie ne peut qu’être utile à la démarche attendue.
Partie A
• Question 1 : des confusions entre forces pressantes et interactions intermoléculaires sont apparues dans cette question.
• Question 2 : les raisonnements en terme énergétique montrant que maintenir une molécule de liquide à l’interface liquide-gaz nécessite un coût énergétique ont également été acceptés par le jury.
• Questions 5 et 6 : de nombreux candidats ne savent pas exprimer correctement la surface d’une sphère ou son volume à partir du rayon.
Partie B
• Questions 15 et 16 : de nombreuses erreurs dans l’attribution des domaines sur le diagramme d’état. Les candidats ayant proposé une attribution correcte n’ont que rarement utilisé correctement le diagramme dans la question suivante pour expliquer l’apparition d’un panache à l’ouverture de la bouteille.14/85
• Question 18 : nombreuses confusions entre concentrations massiques et molaires ainsi que de nombreuses erreurs dans les applications numériques.
• Question 21 : l’utilisation de la loi des gaz parfaits pour expliquer la croissance de la bulle à pression et température constantes n’a pas été systématique.
• Question 22 : la conservation du flux provient du régime stationnaire sans sources. De nombreux candidats se sont lancés dans une démonstration incomplète et chronophage de ce résultat.
• Question 24 : la notion de concentration particulaire est insuffisamment maitrisée par de nombreux candidats.
• Question 26 : la détermination des constantes d’intégration à l’aide des conditions aux limites a parfois posé problème aux candidats.
Partie C
• Question 31 : les conditions d’application de la relation de Bernoulli sont rarement toutes données par les candidats.
• Question 37 : le gradient des vitesses ou taux de cisaillement n’a que rarement été reconnu.
Partie D
• Question 44 : l’appartenance des rayons réfléchis et réfractés au plan d’incidence n’a été mentionnée que dans la moitié des copies.
• Question 45 : étonnamment, peu de candidats ont évoqué et décrit correctement le phénomène de dispersion.
• Question 46 : trop peu de candidats ont identifié des triangles isocèles pour obtenir la relation entre les angles.
• Question 47 : peu de candidats pensent à décomposer le problème en sommant les déviations successives.
Sujet physique G2E 2024
Dans ce sujet, nous nous intéressons à des problèmes physiques liés à la présence de gouttes, bulles et films. La partie A s’intéresse au phénomène de tension superficielle et à la loi de Laplace. La partie B traite de différents aspects des bulles de champagne tandis que la partie C s’intéresse au phénomène de cavitation et à l’implosion d’une bulle. Enfin, la partie D aborde la déviation de la lumière après double réflexion dans une goutte d’eau. Les parties sont indépendantes.
A. TENSION SUPERFICIELLE, COALESCENCE ET LOI DE LAPLACE
Tension superficielle
1. Quelles sont les forces intermoléculaires responsables de la cohésion d’un liquide à molécules aprotiques ? Quelle est leur origine ? Préciser leur caractère attractif ou répulsif.
Ce sont les forces de Van Der Waals, ce sont des forces attractives d’origine électrostatique.
2. On considère deux molécules du liquide : la molécule A est au cœur du liquide et la molécule B à la surface du liquide et du gaz le surplombant. On a représenté également les molécules plus proches voisines de A et de B, avec lesquelles elles sont en interaction. Représenter les différentes forces intermoléculaires s’appliquant sur chaque molécule et en déduire l’origine de la tension superficielle.
Dans le liquide, la molécule A subit des forces égales de toutes les directions.
La molécule B subit moins d’interactions avec les molécules du gaz qu’avec celles du liquide. Il y a un déséquilibre dans les forces et le bilan donne une force orientée vers le bas qui tend à maintenir la molécule dans le liquide.
3. Exprimer l’énergie $𝐸$ associée à la surface $𝑆$ de l’interface liquide-gaz en fonction du coefficient de tension superficielle $𝛾$. Quelle est l’unité S.I. de $𝛾$ ?
$E = \gamma S$
$\gamma = \frac{E}{S} = \frac{[J]}{[m^2]}$ or $1 Joule = 1 kg.m^2.s^{-2}$ $\Rightarrow$ $\gamma = \frac{[kg]}{[s^2]}$
Coalescence de deux gouttes
La coalescence est la fusion de deux gouttes lorsque celles-ci entrent en contact. Le processus est favorable s’il induit une diminution globale de l’énergie du système, ici une diminution de l’énergie de surface. Supposons qu’on étudie la coalescence de deux gouttes de liquide identiques de rayon $𝑅$ pour donner une goutte de rayon $𝑅’$ :
4. En raisonnant sur la minimisation de l’énergie de surface et en négligeant les effets de la pesanteur, justifier pourquoi les gouttes ont une forme sphérique.
La surface d’un volume doit dépenser le moins d’énergie possible et le volume dont la surface est la plus petite est la sphère.
5. En supposant le liquide incompressible, exprimer $𝑅’$ en fonction de $𝑅$.
Utilisons la propriété d’extensivité du volume. On retrouve le même volume avant et après, soit :
$V_1 + V_2 = V’$, or $V_1 = V_2$
$\Rightarrow$ $2 \times \frac{4}{3} \pi R^3 = \frac{4}{3} \pi R’^3$ $\Rightarrow$ $2 R^3 = R’^3$ $\Rightarrow$ $R’= R \sqrt[3]{2}$
6. Déterminer la surface $𝑆’$ de la goutte issue de la coalescence et la comparer à la surface des gouttes de départ. Conclure sur le caractère favorisé ou non de la coalescence.
$S’=4 \pi R’^2= 4 \pi R^2 2^{\frac{2}{3}}$ et $2S=8\pi R^2$
On peut étudier le rapport $\frac{S’}{2S}$ :
$\frac{S’}{2S}= \frac{4 \pi R^2 2^{\frac{2}{3}}}{8 \pi R^2}$ $=\frac{2^{\frac{2}{3}}}{2}<1$
Donc : $S'<2S$, la surface du nouveau volume est plus petite donc l’énergie associée à cette surface également.
7. Représenter une molécule tensioactive à tête polaire et à queue apolaire. Sur un schéma, expliquer comment vont se positionner les tensioactifs à l’interface goutte-liquide dans le cas d’un milieu aqueux et d’une goutte apolaire.
8. Les tensioactifs ont pour effet de diminuer la tension superficielle en se positionnant à l’interface goutte-solution et empêchent la coalescence. Quelle peut être la nature des forces répulsives mises en jeu pour empêcher la coalescence ?
La force répulsive est d’origine électrostatique, les têtes polaires sont de même polarités et se repoussent.
Loi de Laplace
Il existe une différence de pression entre l’intérieur et l’extérieur d’une gouttelette liquide due à l’existence de la tension superficielle qui tend à courber la gouttelette. On considère une gouttelette liquide sphérique (figure ci-dessous à gauche) de rayon $𝑅$ et de pression intérieure $𝑃_i$ en équilibre avec le milieu extérieur de pression $𝑃_e$. On note $∆𝑃 = 𝑃_i – 𝑃_e$ la différence de pression avec $∆𝑃 > 0$.
9. Donner la loi de Laplace exprimant $∆𝑃$ en fonction de $𝛾$ et $𝑅$.
$\Delta P = \frac{2 \gamma}{R}$
10. Calculer $∆𝑃$ dans le cas d’une gouttelette d’eau en suspension dans l’air, de rayon $𝑅 = 50 μ𝑚$ pour laquelle $𝛾_{eau} = 73.10^{−3} S.I (à 20°C)$.
$\Delta P = \frac{2 \gamma}{R}$
Application Numérique :
$\Delta P = \frac{2 \times 73.10^{-3}}{50.10^{-6}} = 2920Pa$
Dans le cas d’une bulle de savon (figure ci-dessus à droite), il y a deux interfaces air – eau liquide : on note $𝑃_i$ la pression de l’air à l’intérieur, $𝑃_{eau}$ la pression de l’eau dans le film de savon
et $𝑃_e$ la pression de l’air extérieur. On note $𝑅_i$ le rayon intérieur, $𝑅_e$ le rayon extérieur du film et $𝛾_{savon} = 25.10^{−3} S.I$. (à 20°C) la tension superficielle de l’interface air – eau savonneuse.
11. Écrire les lois de Laplace pour les deux surfaces intérieure et extérieure puis en déduire l’expression de $∆𝑃 = 𝑃_i – 𝑃_e$ en fonction de $𝛾_{savon}, 𝑅_i et 𝑅_e$.
$P_i – P_{eau} = \frac{2 \gamma _{savon}}{R_i}$ et $ P_{eau} – P_e= \frac{2 \gamma _{savon}}{R_e}$
Soit $\Delta P = P_i – P_e = P_i – P_{eau} + P_{eau} – P_e$ $= \frac{2 \gamma _{savon}}{R_i} + \frac{2 \gamma _{savon}}{R_e}$
12. Simplifier l’expression précédente dans le cas d’un film mince pour lequel $𝑅_i = 𝑅_e = 𝑅$. Calculer $∆𝑃$ avec $𝑅 = 100 μ𝑚$.
Si $R_e = R_i$ alors $\Delta P = \frac{4 \gamma _{savon}}{R}$
Application Numérique :
$\Delta P = \frac{4 \times 25 .10^{-3}}{100.10^{-6}}=1000Pa$
B. DÉTENTE ET CROISSANCE DES BULLES DE CHAMPAGNE
Détente des bulles de champagne lors de l’ouverture de la bouteille
A l’ouverture d’une bouteille de champagne, un panache blanc qui fait penser à des microgouttelettes, se forme. Nous allons proposer une interprétation à ce phénomène. Le gaz présent dans la bouteille est composé principalement de dioxyde de carbone mais contient aussi de l’eau. Il est initialement sous une pression d’environ $𝑃_i = 6,0 bar$ et au moment de l’éjection du bouchon, il subit une détente adiabatique jusqu’à la pression atmosphérique $𝑃_f = 1,0 𝑏ar$ environ.
Pour interpréter simplement le panache, on se place dans le modèle d’une détente adiabatique réversible. Le gaz est supposé parfait, les capacités thermiques du gaz sont supposées indépendantes de la température. On donne l’expression de la variation d’entropie de 𝑛 mol d’un gaz parfait lors d’une transformation le conduisant d’un état initial $(𝑃_i, 𝑇_i)$ à un état final $(𝑃_f, 𝑇_f)$:
$\Delta S = C_P ln(\frac{T_f}{T_i}) – n R ln (\frac{P_f}{P_i})$
où $𝐶_p$ est la capacité thermique à pression constante du gaz.
13. Énoncer le second principe de la thermodynamique. Que vaut la variation d’entropie du gaz lors d’une détente adiabatique réversible ?
Second principe de la thermodynamique :
$\Delta S = S_c + S_e = S_c + \frac{\delta Q}{T}$
Avec $S_e$ : représente l’entropie échangée avec l’extérieur et $S_c$ l’entropie créée au sein du système.
$S_c >0$ pour les transformations irréversibles et $S_c=0$ pour les transformations réversibles.
-Dans le cas d’une détente adiabatique ($S_e=0$) réversible ($S_c=0$), alors $\Delta S = 0$, aussi appelé isentropique
14. Calculer la température $𝑇_f$ du gaz à l’issue de la détente. On donne pour le gaz dans la bouteille : température initiale $𝑇_i = 293 𝐾$ ; capacité thermique molaire à pression constante : $𝐶_P = 37 J. K^{−1}. mol^{−1}$ ; constante des gaz parfaits : $𝑅 = 8,31 J. K^{−1}. mol^{−1}$.
Nous sommes dans le modèle de la détente adiabatique réversible, donc $\Delta S = 0$
$\Rightarrow$ $ C_P ln(\frac{T_f}{T_i}) – n R ln (\frac{P_f}{P_i})=0$ $\Rightarrow$ $C_P ln(\frac{T_f}{T_i}) = n R ln (\frac{P_f}{P_i})$ $\Rightarrow$ $ ln((\frac{T_f}{T_i})^{C_P}) = ln ((\frac{P_f}{P_i})^{nR})$ $\Rightarrow$ $ (\frac{T_f}{T_i})^{C_P} = (\frac{P_f}{P_i})^{nR}$ $\Rightarrow$ $ T_f = T_i \times (\frac{P_f}{P_i})^{\frac{nR}{C_P}}$
Application Numérique :
$ T_f = 293 \times (\frac{1}{6})^{\frac{8,31}{37}} = 196,9K$ soit $-77,1°C$
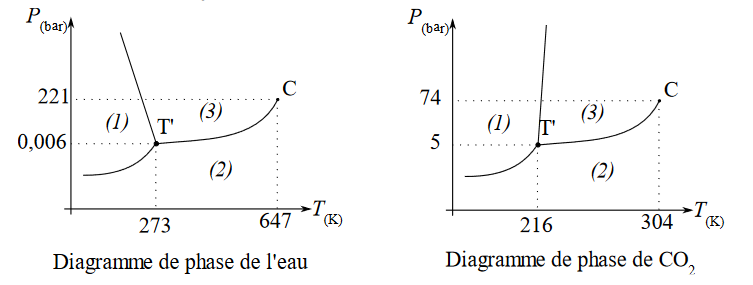
15. On donne ci-dessous les diagrammes de phase de l’eau et du dioxyde de carbone $CO_2$. Préciser les états du système dans les domaines 1, 2 et 3.
L’astuce est d’utiliser le diagramme de l’eau et de se placer à une pression de 1bar. Dans ce cas on sait que lorsque la température augmente, on passe de l’état solide à liquide puis gazeux.
Donc domaine 1 : état solide
domaine 3 : état liquide
domaine 2 : état gazeux
16. En s’appuyant sur les diagrammes précédents, proposer une explication à la formation de panache.
D’après les 2 diagrammes, en passant de l’état initial $P_i=6bar ; T_i = 293K$ à l’état final $P_i=1bar ; T_i = 196K$ l’eau et le $CO_2$ passent de l’état liquide à l’état solide créant un panache composé de glace d’eau et de $CO_2$ en suspension.
17. Pourquoi le modèle proposé n’est-il pas satisfaisant ?
Le modèle n’est pas satisfaisant car le $CO_2$ n’est pas un gaz parfait, On suppose également les capacités thermiques indépendants de la température ce qui n’est pas le cas ici car les variations de températures sont très importantes.
Apparition et croissance des bulles dans le verre par diffusion
Lorsque l’on verse du champagne dans une flûte, une quantité importante de bulles se crée, formant une mousse à la surface libre du liquide. L’expression suivante donne la relation entre la concentration en quantité de matière de dioxyde de carbone dans le champagne et la pression en $Pa$ à la surface libre du champagne dans une situation d’équilibre :
$[CO_2]_{eq} = 0,7 \frac{P}{RT}$
Si la concentration en dioxyde de carbone est supérieure à la concentration d’équilibre $[CO_2]_{eq}$, le liquide est dit sursaturé. La concentration en masse du dioxyde de carbone dans le champagne dans une bouteille fermée est environ égale à $c_c = 12 g.L^{−1}$. On donne la masse molaire du dioxyde de carbone : $𝑀 = 44 g.mol^{−1}$ et la constante des gaz parfaits : $𝑅 = 8,31 J.K^{−1}.mol^{−1}$.
18. Calculer les concentrations en masse du dioxyde de carbone à l’équilibre, à $20 °𝐶$ sous $6 bar$, notée par la suite $𝑐_6$ puis celle à la fin de la détente (conditions ($𝑃_f, 𝑇_f$)), notée $𝑐_f$, et enfin celle à $20 °𝐶$ sous $1 bar$, notée $𝑐_1$. On donnera les valeurs avec deux chiffres significatifs.
Pour calculer directement la concentration en masse, on utilise la formule suivante :
$c = 0,7 \frac{P}{RT} \times \frac{M}{1000}$
pour avoir directement la concentration en $g.L^{-1}$.
Pour $c_6$ :
$c_6 = 0,7 \frac{P}{RT} \times \frac{M}{1000}$
Application Numérique :
$c_6 = 0,7 \frac{6.10^5}{8,31 \times (273+20)} \times \frac{44}{1000}$ $=7,59 g.L^{-1}$
Pour $c_f$ :
Application Numérique :
$c_f = 0,7 \frac{10^5}{8,31 \times 196,9} \times \frac{44}{1000}$ $=1,88 g.L^{-1}$
Pour $c_1$ :
Application Numérique :
$c_1 = 0,7 \frac{10^5}{8,31 \times (273+20)} \times \frac{44}{1000}$ $=1,26 g.L^{-1}$
19. Montrer que les résultats précédents permettent de justifier qu’une détente entraîne a priori la formation de bulles à la surface du liquide.
Quand la bouteille est fermée, le champagne est sursaturé en dioxyde de carbone. Lorsque le bouchon saute et que la pression descend subitement à 1 bar, le dioxyde de carbone se libère en formant un panache de bulle.
Une fois le champagne versé, on observe des chapelets de bulles au sein d’une flute de champagne. L’apparition de ces bulles est principalement due à la présence de fibres de cellulose provenant de particules en suspension dans l’air voire du chiffon utilisé pour essuyer la flûte. Ces fibres de cellulose possèdent une cavité qui renferme de l’air. Les molécules de CO2 dissous en phase aqueuse vont diffuser vers la poche d’air. Celle-ci va grossir jusqu’à atteindre une extrémité de la poche et former alors une bulle.
La pression de l’air dans la poche d’air est prise égale à $1,0 bar$ dans une situation d’équilibre et on se place à $20 °𝐶$.
20. Justifier la diffusion des molécules de $CO_2$ de la phase aqueuse vers la poche d’air.
Réponse
La concentration du $CO_2$ à l’équilibre est $c_c = 12g.L^{-1}$, soit : $c_c = 12 \times \frac{1000}{44} = 272,7 mol.m^{-3}$
Or la concentration de l’air dans les conditions établies dans l’énoncé est :
$C_{air} = \frac{n}{V} = \frac{P}{RT}$
Application Numérique :
$C_{air} = \frac{10^5}{8,31 \times (273+20)} = 41,1mol.m^{-3}$
La concentration du $CO_2$ est donc supérieure à celle de l’air, il y a diffusion de l’élément le plus concentré vers l’élément le moins concentré, donc une diffusion des molécules de $CO_2$ vers la poche d’air.
21. Justifier alors que la poche d’air grossit dans les conditions expérimentales retenues
Réponse
Il y a une augmentation de molécules dans un volume délimité par la fibre de cellulose, la pression va augmenter et ainsi le volume de la poche {air + $CO_2$ } augmentera.
Une fois la bulle formée, elle se détache de la fibre et monte dans le liquide dans lequel elle va grossir. Nous allons étudier cette augmentation de taille. Quand elle se détache de la fibre, la pression au sein de la bulle est égale à 1 bar. La bulle est supposée sphérique de rayon $𝑅_b$.
On considère que la concentration en $CO_2$ dissous vaut $c_c$ loin de la bulle et $𝑐_1$ pour $r = 𝑅_b$. On suppose dans un premier temps que $𝑅_b$ est constant et on se place en régime stationnaire.
22. Justifier qu’un flux $Φ$ de dioxyde de carbone se met en place au sein du champagne liquide et montrer que ce flux se conserve.
Réponse
La différence de concentration dans le champagne (loin de la bulle et sur la surface de la bulle) permet la création d’un flux de dioxyde de carbone des concentrations les plus élevée vers la concentration la moins élevée. Les valeurs $c_c$ et $c_1$ restent constante au fil du temps ce qui a pour conséquence un flux qui se conserve.
23. Donner la loi de Fick dans le contexte étudié en précisant la signification physique des différents termes ainsi que leurs unités. On notera $𝑛^∗(𝑏)$ la concentration particulaire du $CO_2$, $r$ étant la distance au centre de la bulle avec $r > 𝑅_b$ et $𝐷$, le coefficient de diffusion du dioxyde de carbone dans le champagne liquide.
Réponse
Loi de Fick : (attention en coordonnées polaires)
$\Phi = – D \frac{\delta n^*}{\delta r} S$
avec $\Phi$ le flux particulaire traversant une surface S par unité de temps ($s^{-1}$) ; D coefficient de diffusion en $m^2.s^{-1}$ ; $n^*$ densité particulaire $m^{-3}$ ; r en (m) ; S la surface à travers laquelle passe le flux en $m^2$
Dans les questions suivantes, on introduit la constante d’Avogadro $𝒩_a$.
24. Donner la relation entre la concentration en masse de $CO_2$ en solution $𝑐, 𝑛^∗, 𝒩_a$ et la masse molaire $𝑀$ du dioxyde de carbone.
Réponse
On rappelle les formules de base nécessaire :
$n= \frac{N}{N_A}$ ; $M = \frac{m}{n}$ et $n^* = \frac{N}{V}$
Or, $c=\frac{m}{V} = \frac{nM}{V}$ $=\frac{N M}{N_A V} = \frac{n^* M}{N_A}$
25. Montrer que la concentration en masse $𝑐(r)$ au sein du champagne liquide vérifie l’équation : $\frac{𝑑𝑐}{𝑑r} = \frac{A}{4𝜋Dr^2}$, où $𝐴$ est une constante que l’on exprimera en fonction $Φ,𝒩_a et 𝑀$.
Réponse
On a :$\Phi = – D \frac{\delta n^*}{\delta r} S$ (question 23) et $c= \frac{n^* M}{N_A}$ (question 24) soit $n^* = \frac{cN_A}{M}$
$\Rightarrow$ $\Phi = – D \frac{N_A\delta c}{ M \delta r} S$ $\Rightarrow$ $\frac{dc}{dr} = \frac{- \Phi M}{D N_A S}$ avec $S=4\pi r^2$ (surface de la sphère de rayon r à travers laquelle passe le flux)
$\Rightarrow$ $\frac{dc}{dr} = \frac{- \Phi M}{D N_A 4 \pi r^2}$ $=\frac{A}{4\pi D r^2}$ avec $A= \frac{-\Phi M}{N_A}$
26. Établir l’expression suivante de $𝑐(r) : 𝑐(r) = (𝑐_1 − 𝑐_c) \frac{𝑅_b}{r} +𝑐_c$ pour $r > 𝑅_b$.
Réponse
$\frac{dc}{dr} = \frac{A}{4\pi D r^2}$ $\Rightarrow$ $dc = \frac{A}{4\pi D r^2} dr$
Pour retrouver c(r) en fonction de $c_C$ on intègre entre les bornes de rayon r et l’infini
$\int_{c_C}^{c(r) }dc = \frac{A}{4\pi D } \int_{\infty}^r \frac{dr}{r^2}$ $\Rightarrow$ $c(r) -c_C = \frac{A}{4\pi D } [- \frac{1}{r}]_{\infty}^r $ $= \frac{A}{4\pi D } [- \frac{1}{r} + 0]$ donc : $c(r) = -\frac{A}{4\pi D r} + c_C$
Si maintenant on intègre entre les bornes $c_1$ et $c_C$, on obtient :
$\int_{c_1}^{c_C }dc = \frac{A}{4\pi D } \int_{R_b}^{\infty} \frac{dr}{r^2}$ $\Rightarrow$ $c_C – c_1 = \frac{A}{4\pi D } [- \frac{1}{r}]_{R_b}^{\infty} $ $=\frac{A}{4\pi D } \frac{1}{R_b} $ soit : $(c_C – c_1)R_b = \frac{A}{4 \pi D}$
On obtient alors :
$c(r) = -\frac{A}{4\pi D r} + c_C$ $= -(c_C – c_1)\frac{R_b }{ r} + c_C$ $=(c_1 – c_C)\frac{R_b }{ r} + c_C$
Le régime n’est en réalité pas stationnaire. Nous utiliserons néanmoins l’expression trouvée dans la question 26 en prenant en compte le fait que le rayon $𝑅_b(𝑡)$ dépend du temps.
27. En supposant que toutes les molécules de dioxyde de carbone arrivant à la surface de la bulle y pénètrent, montrer que le flux moléculaire, qui s’identifie au taux de variation $Φ = \frac{𝑑𝑁_g}{dt}$ du nombre $𝑁_g$ de molécules de dioxyde de carbone dans la bulle, admet comme expression $\frac{𝑑𝑁_g}{𝑑t} = \frac{𝒩_a 𝑃}{𝑅T} \frac{𝑑V}{dt}$ , où $𝑃 et 𝑇$ sont la pression et la température de la bulle supposées constantes, et $\frac{𝑑V}{dt}$ le taux de variation du volume.
Réponse
Dans la bulle, à chaque instant on a:
$P V(t) = n_g (t) RT$, soit $n_g(t) = \frac{N_g(t)}{N_A}= \frac{P V(t)}{RT}$ $\Rightarrow$ $N_g(t) = \frac{N_A P V(t)}{RT}$ $\Rightarrow$ $\frac{d N_g(t)}{dt } = \frac{P N_A}{RT} \times \frac{dV(t)}{dt}$
28.En déduire la relation : $𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$ dont on vérifiera l’homogénéité.
Réponse
Le flux arrivant dans la bulle depuis le champagne est égal au taux de variation de $CO_2$ dans la bulle car on considère que toutes les molécules de dioxyde de carbone pénètrent.
On a donc : $\frac{dN_g}{dt} = \frac{N_A P}{RT} \frac{dV}{dt} = \frac{D N_A S}{M} \frac{dc}{dr}$ avec $\frac{dc}{dr}=(c_1-c_C)R_b (\frac{-1}{r^2})$ et $V=\frac{4}{3}\pi R_b^3$ soit $\frac{dV}{dt}= 4\pi R_b^2 \frac{d R_b}{dt}$
$\Rightarrow$ $\frac{N_A P}{RT} 4\pi R_b^2 \frac{d R_b}{dt}=\frac{D N_A 4 \pi r^2}{M} (c_1-c_C)R_b (\frac{-1}{r^2}) $ $\Rightarrow$ $𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$
29. On néglige le volume initial de la bulle, de sorte que $𝑅_b(𝑡 = 0) ≈ 0$. En déduire $𝑅_b(𝑡)$.
Réponse
$𝑅_b \frac{𝑑𝑅_b}{𝑑𝑡} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀}$ $\Rightarrow$ $𝑅_b 𝑑𝑅_b = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇 dt}{𝑃𝑀}$ $\Rightarrow$ $\int_0^{R_b(t)} 𝑅_b 𝑑𝑅_b =\int_0^{t} \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇 dt}{𝑃𝑀}$ $\Rightarrow$ $ [\frac{𝑅_b ^2}{2}]_0^{R_b(t)} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} [t]_0^{t} $ $\Rightarrow$ $ \frac{𝑅_b(t) ^2}{2} = \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t $ $\Rightarrow$ $ 𝑅_b(t) = \sqrt{2 \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t }$
30. On donne en plus des valeurs numériques précédentes : $𝐷 = 3.10^{−9} 𝑆.𝐼.$ Calculer en $𝑚s$ la durée $∆𝑡$ mise par une bulle pour atteindre un rayon de $10 μm$.
Réponse
$ 𝑅_b(t) = \sqrt{2 \frac{(𝑐_c−𝑐_1 )𝐷𝑅𝑇}{𝑃𝑀} t }$
Application Numérique :
$R_b(t) = \frac{(10.10^{-6})^2 \times 10^5 \times 44.10^{-3}}{2 \times (12-1,26) \times 3.10^{-9} \times 8,31 \times (273+20)} = 2,8ms$
C. IMPLOSION D’UNE BULLE
On s’intéresse au phénomène de cavitation : il s’agit de la naissance de bulles de gaz ou de vapeur dans un liquide soumis à une dépression. Si cette dépression est suffisamment importante, la pression peut devenir inférieure à la pression de vapeur saturante $𝑃_{sat}$ et une bulle de vapeur est susceptible de se former. Celle-ci va imploser et voir son rayon passer d’une valeur initiale $𝑅_0$ à zéro.
La cavitation est responsable du phénomène d’embolie gazeuse chez les arbres en période de grande sécheresse pouvant entrainer la mort des arbres. Dans cette étude, on considérera l’ensemble des phénomènes mis en jeu comme isothermes et on négligera tout phénomène de transferts thermiques.
Modèle simple d’implosion
On suppose qu’initialement la bulle de gaz a pour rayon $𝑅_0$ et contient du gaz à la pression $𝑃_{sat}$.
Le liquide, de masse volumique $ρ$ constante, s’écoule autour de la bulle immobile. Loin de la bulle, la pression du liquide est supposée constante et égale à $𝑃_0 > 𝑃_{sat}$.
On appelle vitesse radiale de l’interface liquide/gaz matérialisant la bulle, la dérivée temporelle de $𝑅_(𝑡) : 𝑣 = \frac{𝑑𝑅}{𝑑𝑡}$ . On néglige tout phénomène de tension superficielle ainsi que les forces de pesanteur et on suppose qu’on se place, du point de vue du liquide, dans les conditions d’application de la relation de Bernoulli.
31. Rappeler les conditions d’application de la relation de Bernoulli et l’appliquer sur une ligne de courant horizontale allant du cœur du liquide à la bulle de rayon $𝑅$. On supposera que le liquide en contact avec la bulle est à la pression $𝑃_{sat}$.
Réponse
Conditions d’application de la relation de Bernoulli :
Le fluide doit être parfait avec une masse volumique constante (fluide incompressible). Le régime doit être stationnaire. Il ne doit pas y avoir de travail utile (W’=0 : machine extérieure) ni d’échange thermique avec l’extérieur (Q=0).
Dans ces conditions on a :
$\Delta (\frac{1}{2} v^2 + gz + \frac{P}{\rho})=0$
soit :
$\frac{1}{2} v_L^2 + g z_L + \frac{P_0}{\rho} = \frac{1}{2} v_R^2 + g z_R + \frac{P_{sat}}{\rho}$
32. En déduire la vitesse radiale $𝑣$ de l’implosion. On s’attachera à bien respecter le signe de $𝑣$.
Réponse
$\frac{1}{2} v_L^2 + g z_L + \frac{P_0}{\rho} = \frac{1}{2} v_R^2 + g z_R + \frac{P_{sat}}{\rho}$ avec $z_R = Z_L$ et $V_L=0$ ce qui revient à : $ \frac{P_0}{\rho} = \frac{1}{2} v_R^2 + \frac{P_{sat}}{\rho}$ $\Rightarrow$ $V_R = \sqrt{\frac{2}{\rho} (P_0 – P_{sat})}$
Application Numérique :
$V_R = \sqrt{\frac{2}{1,0.10^3} (1 -0,032).10^5} = 13,9m.s^{-1}$ or $V_R$ est négatif car le rayon diminue avec le temps donc $\frac{dR}{dt}<0$. Donc $V_R = – 13,9m.s^{-1}$
33. En supposant $𝑣$ constante, en déduire la loi horaire $𝑅(𝑡)$.
Réponse
Soit $v= \frac{dR}{dt} = cte =A$ $\Rightarrow$ $R(t) = At + R_0$
34. En déduire le temps $τ$ d’implosion de la bulle en fonction de $ρ$, $𝑅_0$, $𝑃_0$ et $𝑃_{sat}$
Réponse
On cherche $\tau$ tel que $R(\tau) = 0 = A \tau + R_0$ Soit : $A\tau= – R_0$ $\Rightarrow$ $\tau = – \frac{R_0}{A}= – \frac{R_0}{\sqrt{\frac{2}{\rho} (P_0 – P_{sat})}}$
35. Calculer $τ$ avec : $𝑅_0 = 1,0 mm$ ; $𝑃_0 = 1,0 bar$ ; $𝑃_{sat} = 0,032 bar$ ; $ρ = 1,0.10^3 kg.m^{−3}$.
Réponse
Application Numérique :
$\tau = – \frac{1,0.10^{-3}}{-13,9} = 0,0848s =8,5ms$
Modélisation à l’aide de l’équation de Rayleigh-Plesset
La modélisation précédente n’est pas satisfaisante car elle ne tient pas compte du transfert de masse au cours de l’implosion de la bulle. Ainsi la vitesse $𝑣(𝑡)$ dépend du temps et l’évolution temporelle de la bulle de vapeur de rayon $𝑅(𝑡)$ est donnée par l’équation de Rayleigh-Plesset, dans l’hypothèse où on peut négliger la contribution des gaz non condensables tels que $O_2$ ou $N_2$ :
$ρ(𝑅\ddot{R} + \frac{3}{2} \dot𝑅^2) = 𝑃_{sat} − 𝑃_0 − \frac{2𝛾}{𝑅} − 4𝜂\frac{\dot R}{𝑅}$
Dans le membre de gauche, figurent : $𝑅$ le rayon de la bulle, $𝑣 = \dot{R}$ la vitesse radiale et $\ddot{R}$ sa dérivée par rapport au temps. Dans le membre de droite, apparaissent trois termes :
$\Rightarrow$ $𝑃_{sat} − 𝑃_0 $ représente la différence entre la pression de vapeur saturante et la pression du liquide loin de la bulle. C’est le principal moteur responsable de la croissance de la bulle ou de son implosion.
$\Rightarrow$ Le terme $− \frac{2𝛾}{𝑅}$ représente l’effet de la tension superficielle.
$\Rightarrow$ Le terme $−4𝜂 \frac{\dot{R}}{𝑅}$ représente l’effet des forces de viscosité avec $η$ la viscosité dynamique.
36. Que devient l’équation de Rayleigh-Plesset en régime stationnaire ? Quelle loi retrouve- t- on ?
Réponse
En régime stationnaire : $\dot R = \ddot R = 0$
L’équation devient :
$0= 𝑃_{sat} − 𝑃_0 − \frac{2𝛾}{𝑅} $, soit $\frac{2𝛾}{𝑅} = 𝑃_{sat} − 𝑃_0 = \Delta P $ , on reconnait la loi de Laplace (ou équation de Laplace-Young) reliant tension superficielle et différence de pression.
37. Dans le terme de viscosité, que représente la grandeur $\frac{\dot R}{𝑅}$ ? Donner l’unité S.I. de la viscosité dynamique $η$.
Réponse
$\frac{\dot R}{𝑅}$ représente le gradient de vitesse (ou profil de vitesse).
L’unité S.I. de la viscosité dynamique $\eta$ :
Les termes d’une somme doivent avoir la même unité donc dans l’expression $ρ(𝑅\ddot{R} + \frac{3}{2} \dot𝑅^2) = 𝑃_{sat} − 𝑃_0 − \frac{2𝛾}{𝑅} − 4𝜂\frac{\dot R}{𝑅}$ il suffit de prendre le terme contenant $\eta$ et un terme dont on connait l’unité, par exemple : $ρ \frac{3}{2} \dot𝑅^2 $ on a alors une homogénéité des unités pour $ρ\frac{3}{2} \dot𝑅^2 \sim 4𝜂\frac{\dot R}{𝑅}$. Les constantes peuvent être supprimées car elles n’interviennent pas dans l’unité, on a alors : $ρ \dot𝑅^2 \sim 𝜂\frac{\dot R}{𝑅}$ $\Rightarrow$ $\eta \sim \rho \dot R R$ $\Rightarrow$ $[\eta] \sim \frac{[M]}{[L^3]} \frac{[L]}{[T]} [L] = [M].[L]^{-1}.[T]^{-1}$, soit : ($kg.m^{-1}.s^{-1}$)
On néglige par la suite le terme de viscosité.
38. On se place en régime variable et on étudie des bulles de rayon initial $𝑅_0$. À quelle condition sur $𝑅_0$, peut-on négliger le terme de tension superficielle ? Simplifier alors l’équation précédente.
Réponse
On sait que $P_{sat} -P_0$ est de l’ordre de l’unité, si $\frac{2 \gamma}{R} << 1$ alors le terme est négligeable soit : $\frac{2 \gamma}{R} < 0,1$ $\Rightarrow$ $2 \gamma < \frac{R}{10}$ $\Rightarrow$ $R > 20 \gamma $
L’équation devient :
$ρ(𝑅\ddot{R} + \frac{3}{2} \dot𝑅^2) = 𝑃_{sat} − 𝑃_0 $
39. En multipliant l’équation précédente par $𝑅^2$ et en remarquant que :
$\frac{𝑑(𝑅^3 \dot 𝑅^2)}{𝑑𝑅} = 3 \dot R^2 𝑅^2 + 2𝑅^3 \ddot R$, intégrer l’équation précédente avec les conditions initiales suivantes : $𝑅(𝑡 = 0) = 𝑅_0$, $ \dot R(𝑡 = 0) = 0$ et montrer que : $\dot R^2 = \frac{2}{3} \frac{𝑃_{sat} − 𝑃_0}{𝜌} [1 − (\frac{R_0}{R})^3]$.
Réponse
$R^2 \times ρ(𝑅\ddot{R} + \frac{3}{2} \dot𝑅^2) = R^2 \times (𝑃_{sat} − 𝑃_0 )$ $\Rightarrow$ $ ρ(𝑅^3 \ddot{R} + \frac{3}{2} R^2 \dot𝑅^2) = R^2 \times (𝑃_{sat} − 𝑃_0 )$ $\Rightarrow$ $ 2 𝑅^3 \ddot{R} + 3 R^2 \dot𝑅^2 =\frac{2}{\rho} R^2 \times (𝑃_{sat} − 𝑃_0 )$ $\Rightarrow$ $ \int ( 2 𝑅^3 \ddot{R} + 3 R^2 \dot𝑅^2) =\int (\frac{2}{\rho} R^2 \times (𝑃_{sat} − 𝑃_0 ))$ $\Rightarrow$ $R^3 \dot R^2 = \frac{2 (P_{sat} – P_0)}{ \rho} \frac{R^3}{3}+ cte$
Calcul de la constante :
on reprend les conditions initiales et on obtient : $0= \frac{2 (P_{sat} – P_0) R_0^3}{3 \rho} + cte$, soit : $cte = -\frac{2 (P_{sat} – P_0) R_0^3}{3 \rho}$
$\Rightarrow$ $R^3 \dot R^2 = \frac{2 (P_{sat} – P_0)}{ 3 \rho} (R^3 – R_0^3)$ soit $ \dot R^2 = \frac{2 (P_{sat} – P_0)}{ 3 \rho} (1 – (\frac{R_0}{R})^3 )$
40. En déduire l’expression de $\dot R$ lorsque $P_0 > 𝑃_{sat}$
Réponse
Rappelons nous tout d’abord que $\dot R<0$ (question 32). On peut également changer le signe de $(P_{sat} – P_0)$ et de $ (1 – (\frac{R_0}{R})^3 )$ pour anticiper sur la racine qu’il faudra séparée par la suite (la valeur sous la racine doit être positive)
On réécrit alors $(- \dot R)^2 = \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho} [(\frac{R_0}{R})^3 -1]$ $\Rightarrow$ $ \dot R =- \sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho} [(\frac{R_0}{R})^3 -1]}$
41. Par séparation des variables et en utilisant l’intégrale $\int_0^1 \sqrt{\frac{U^3}{1-U^3}} dU = 0,747$, montrer que le temps d’implosion de la bulle vaut : $ \tau = 0,915 𝑅_0 \sqrt{ \frac{𝜌}{𝑃_0−𝑃_{sat}}}$ .
Réponse
$- \frac{dR}{dt} =\sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho} [(\frac{R_0}{R})^3 -1]}$ $\Rightarrow$ $- \frac{dR}{dt} =\sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho}} \sqrt{ [(\frac{R_0}{R})^3 -1]}$ $\Rightarrow$ $\frac{- dR}{ \sqrt{ [(\frac{R_0}{R})^3 -1]}} =\sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho}} dt $
Or, $\frac{- dR}{ \sqrt{ [(\frac{R_0}{R})^3 -1]}} =\frac{- dR}{ \sqrt{ [(\frac{R_0^3 – R^3}{R^3})]}} = -dR \sqrt{ [(\frac{ R^3}{R_0^3 -R^3})]}$
On applique un changement de variables en prenant $U=\frac{R}{R_0}$, donc $dU = \frac{dR}{R_0}$
ce qui donne : $-R_0 dU \sqrt{\frac{U^3}{1 – U^3}} = \sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho}} dt $
Attention aux bornes d’intégration U vaut 1 pour $R=R_0$ à $t=0$ et U vaut $0$ pour $R=0$ soit $t=\tau$.
$\int_0^1 {-R_0 dU \sqrt{\frac{U^3}{1 – U^3}}} =\int_{\tau}^0 { \sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho}} dt }$ $\Rightarrow$ $-R_0 \times 0,747 = \sqrt{ \frac{2}{3} \frac{(P_0 – P_{sat})}{\rho}} (- \tau)$ $\Rightarrow$ $\tau = R_0 \times 0,747 \sqrt{ \frac{3}{2} \frac{\rho}{(P_0 – P_{sat})}} $ $= 0,915 R_0\sqrt{ \frac{\rho}{(P_0 – P_{sat})}} $
42. Calculer $τ$ avec : $𝑅_0 = 1,0 mm$ ; $𝑃_0 = 1,0 bar$ ; $𝑃_{sat} = 0,032 bar$ ; $ρ = 1,0.10^3 kg.m^{−3}$ et comparer au résultat de la question 35.
Réponse
Application Numérique :
$\tau = 0,915 \times 1,0.10^{-3} \sqrt{\frac{1,0.10^3}{(1,0 – 0,032).10^5}}= 9,3.10^{-5} s$ soit un temps bien plus vourt que celui de la question 35.
43. Que vaut la vitesse radiale au moment de l’implosion ? Critiquer alors la pertinence du modèle précédent
Réponse
On reprend le l’équation de la question 38 : $ρ(𝑅\ddot{R} + \frac{3}{2} \dot𝑅^2) = 𝑃_{sat} − 𝑃_0 $ avec comme condition, $R(\tau)=0$ il reste : $ρ \frac{3}{2} \dot𝑅^2 = 𝑃_{sat} − 𝑃_0 $ $\Rightarrow$ $-\dot R^2 = \frac{2 (P_{sat}-P_0)}{3 \rho}$(vitesse négative)$\Rightarrow$ $ \dot R = \sqrt{\frac{2 (P_0 -P_{sat})}{3 \rho}}$
Application Numérique :
$ \dot R = \sqrt{\frac{2 (1 – 0,032).10^5}{3 \times 10^3}}= 8m.s^{-1}$
D. DÉVIATION DE LA LUMIÈRE DANS UNE GOUTTE D’EAU
On cherche à calculer la déviation $𝐷$ d’un rayon lumineux provoquée par deux réflexions à l’intérieur d’une goutte d’eau (voir schéma ci-dessous). L’angle $𝐷$ est l’angle entre le rayon sortant et le rayon entrant dans la goutte. On constate une dispersion des rayons de la lumière blanche à l’intérieur de la goutte d’eau.
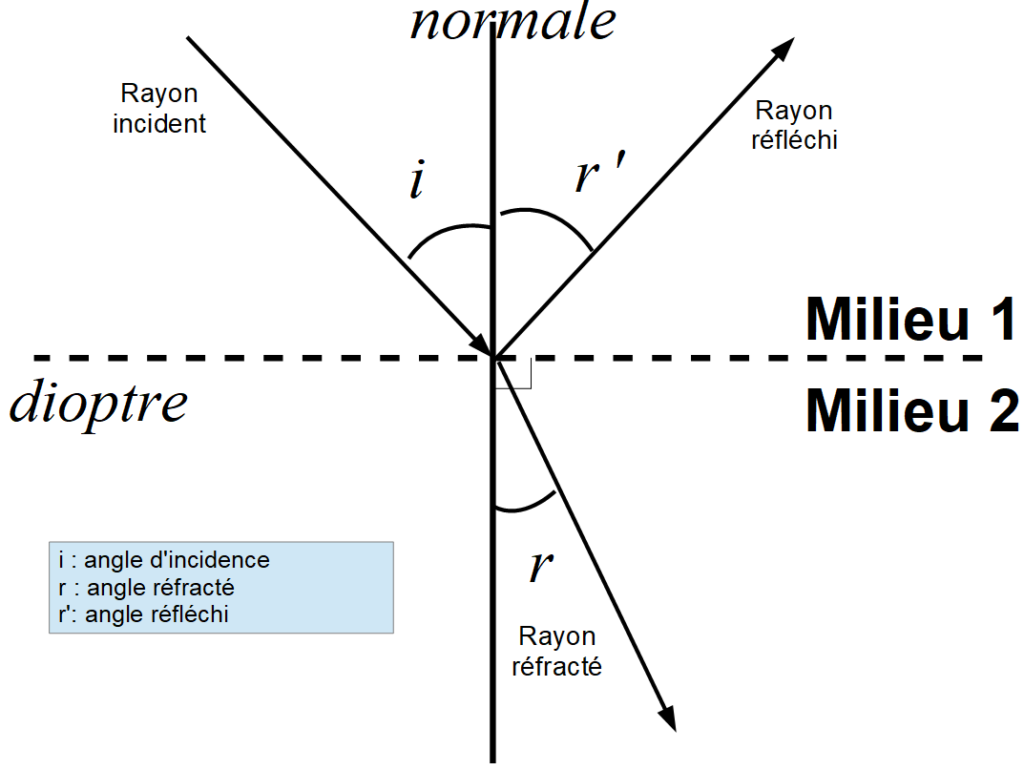
44. Rappeler les lois de Descartes de la réflexion et de la réfraction. On notera $𝑖$ l’angle d’incidence et $𝑏$ l’angle de réfraction (angles comptés positivement et non algébriques). On illustrera le propos par des schémas annotés
Réponse
Lois de Descartes :
Loi de la réflexion : Le rayon incident, la normale au dioptre et le rayon réfléchi sont contenus dans le même plan d’incidence. Les angles incidents $i$ et réfléchis $r’$ sont égaux en valeur absolus : $i = r’$
Loi de la réfraction : Le rayon incident, la normale au dioptre et le rayon réfléchi sont contenus dans le même plan d’incidence. La relation liant les indices de réfraction $n_1$ et $n_2$ de chacun des milieux et les angles incidents $i$ et réfracté $r$ s’écrit :
$n_1 sin(i) = n_2 sin(r)$
45. Préciser en quoi consiste la dispersion des rayons lumineux.
Réponse
La dispersion des rayons lumineux correspond aux changements de directions que peut prendre un rayon lumineux composé de plusieurs longueurs d’ondes différentes. L’angle de réfraction dépend de la longueur d’onde. Cela provient du fait que les ondes ne se déplacent pas à la même vitesse au sein d’un milieu dispersif.
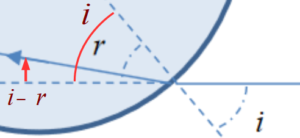
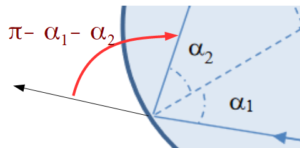
46. Exprimer les angles $\alpha_j$ ($j = 1 à 6$ sur le schéma de la goutte) en fonction de $𝑖$ et de $r$.
Réponse
$\alpha_1 = r$, car on se trouve dans un triangle isocèle passant par O avec $\alpha_1 et r$ comme angle à la base et les 2 cotés égaux partant de O qui sont les rayons.
$\alpha_1$ et $\alpha_2$ sont égaux car il y a réflexion dans la goutte donc les angles sont égaux (loi de la réflexion)
$\alpha_2$ et $\alpha_3$ sont égaux (triangle isocèle)
$\alpha_3$ et $\alpha_4$ sont égaux(loi de la réflexion)
$\alpha_4$ et $\alpha_5$ sont égaux (triangle isocèle)
$\alpha_6 = i$ car on sort de la goutte en appliquant la loi de la réfraction avec comme angle incident $r$
Au final : $\alpha_1 = \alpha_2 = \alpha_3= \alpha_4= \alpha_5 =r$ ; $\alpha_6 = i$
47. Montrer que l’angle de déviation $𝐷$ s’écrit : $𝐷 = 2\pi + 2𝑖 – 6r$.
Réponse
On décompose les changements de directions depuis l’origine du rayon incident :
Une première déviation angulaire de $i-r$
Une deuxième déviation angulaire de $\pi – \alpha_1 – \alpha_2 = \pi – 2r$
Une troisième déviation angulaire de $\pi – \alpha_3 – \alpha_4 = \pi – 2r$
Une quatrième déviation équivalente à la première car on ressort de la goutte : $i-r$
La somme des déviations nous donne $D = i-r + \pi -2r + \pi -2r + i -r = 2\pi +2i -6r$
48. On se propose de déterminer numériquement la valeur de l’angle d’incidence $𝑖_𝑃$ telle que les rayons incidents et réfléchis par la goutte soient perpendiculaires. On constate par ailleurs que le minimum de déviation vaut $𝐷_{min} = 241°$. On utilise un programme Python utilisant la fonction $fsolve$. Compléter ce programme en donnant l’expression de la fonction f retenue, écrite en langage python. On prendra $𝑛_r = 1,3317$, l’indice de réfraction de l’eau pour une lumière rouge.
Données
La fonction fsolve du module scipy.optimize permet la résolution d’une équation de la forme f(x) = 0. Elle nécessite l’importation du module correspondant. La fonction f doit être définie au préalable et la valeur initiale $x_0$ de l ‘algorithme doit être précisée (valeur initiale à partir de laquelle le module recherche le zéro de la fonction). Syntaxe à utiliser :
import scipy.optimize as op
op.fsolve(f,x0)
np.arcsin(x) donne en radians la valeurs de l’angle x, compris entre -π/2 et π/2, dont on connaît le sinus.
math.degrees(a) donne la valeur de l’angle a en degrés à partir de sa valeur en radians
Programme python à compléter
import scipy.optimize as op
import numpy as np
import math
Pi = math.pi
def f(x) :
return À COMPLÉTER
x0 = 0
zero = op.fsolve(f,x0)
iP = math.degrees(zero)
print(« La valeur de iP recherchée en degrés proche de « ,x0, » est « ,iP , » »)
L’exécution du programme donne :
La valeur de iP recherchée en degrés, proche de 0, est 38.39
Réponse
La déviation est de $\frac{3 \pi}{2}$ pour que les rayons incident et réfléchis forment un angle droit.
La déviation est donnée par :
$D =2\pi +2i -6r = 2\pi +2i -6(arcsin(\frac{sin(i)}{1,3317}))$
La fonction op.solve permet de trouver la solution à une équation pour laquelle $f(x)=0$, or nous souhaitons trouver la solution pour $D = \frac{3 \pi}{2}$ . Il faut donc rechercher la solution pour $D – \frac{3 \pi}{2} = 0$
La ligne à ajouter dans la fonction est :
return 2*Pi + 2*x – 6*(np.arcsin(np.sin(x)/1.3317)) – 3*Pi/2