Physique BCPST2
Mécanique des fluides | Ecoulement Poiseuille
Extrait du sujet 2023 A BCPST voir le sujet corrigé complet
3. Quelques propriétés hydrodynamiques des glaciers
Du fait de leur plasticité, les glaciers s’écoulent lentement sous l’effet de la gravité avec une vitesse d’écoulement très variable selon la pente, la topographie du lit rocheux ou l’épaisseur de la glace. La vitesse moyenne est de l’ordre de quelques centimètres à quelques dizaines de centimètres par jour, le record revenant au glacier Kangerdlugssuaq dans le Groënland où la vitesse moyenne atteinte est de 14 kilomètres par an. Par ailleurs, les glaciers ne sont pas des masses compactes de glace. Ils sont traversés par un réseau hydrographique de canaux qui collectent et véhiculent l’eau liquide formée en surface.
Cette partie propose d’étudier, sur la base du modèle de Poiseuille, l’écoulement d’un glacier sous l’effet de la gravité et d’interpréter certains aspects du réseau hydrographique interne au glacier grâce au modèle de Roethlisberger.
I. L’écoulement de Poiseuille dans une conduite cylindrique.
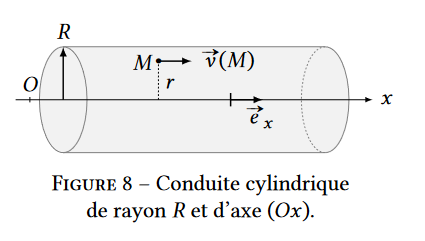
On considère l’écoulement stationnaire d’un fluide visqueux newtonien de viscosité dynamique 𝜂, incompressible de masse volumique 𝜌, dans une conduite cylindrique horizontale de rayon 𝑅 et d’axe de symétrie de révolution (𝑂𝑥). Il règne dans la conduite un gradient horizontal de pression noté $\frac{dp}{dx}$ (avec $\frac{dp}{dx}$ < 0), supposé indépendant de 𝑥. En un point 𝑀 de l’écoulement, la vitesse d’écoulement du fluide s’écrit : $\vec{v} (M) = v(r) \vec e_x$, où 𝑟 est la distance entre le point 𝑀 et l’axe (𝑂𝑥) et $\vec{e_x}$ un vecteur unitaire orientant l’axe (𝑂𝑥) (voir figure 8).
On admet que le fluide adhère aux parois de la conduite, ce qui se traduit par : 𝑣(𝑟 = 𝑅) = 0.
28. À l’aide d’un bilan de quantité de mouvement appliqué à un système fermé à définir, établir l’expression suivante de la vitesse d’écoulement, en prenant soin d’expliciter chaque étape du raisonnement :
$\vec{v} (M)= \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} \vec e_x$ (1)
La force de viscosité $\vec 𝑓_v$ que le fluide situé à l’extérieur du cylindre de rayon $𝑟$, de longueur $𝐿$ et d’axe $(𝑂𝑥)$ exerce sur le fluide contenu dans ce cylindre s’écrit : $\vec f_v = 2 \pi r L \eta \frac{dv}{dr} \vec e_x$
On considère la portion de fluide cylindrique, de rayon r et de longueur dx, centrée sur l’axe.
On note $P_e$ la pression à l’entrée de cette portion de fluide et $P_s$ la pression en sortie. Soit $dp = P_s – P_e)$
On applique le théorème de la résultante cinétique au système constitué de cette portion de fluide à l’instant $t$ et de la masse $dm$ qui y rentre entre les instants $t$ et $t + dt$.
A l’instant $t + dt$, ce système est constitué de la même portion de fluide contenu dans le cylindre de rayon $r$ et de la masse $dm$ qui en est sortie entre les instants $t$ et $t + dt$.
En régime stationnaire, la variation de quantité de mouvement de ce système fermé est alors simplement nulle.
Par conséquent, la somme des forces qui s’exercent sur ce système est également nulle :
$\sum{\vec F} = \vec 0$
Soit la force de pression en amont, $\pi r^2 P_e$, moins la force de pression en aval, $\pi r^2 P_s$ plus la force de frottement visqueuse F qui s’exerce sur la surface latérale du cylindre de rayon r qui est égale à 0 :
$\pi r^2 P_e – \pi r^2 P_s + F = 0$
Pour un fluide visqueux newtonien, la force de viscosité F est donnée par:
$F = \eta \frac{d v(r)}{dr} 2 \pi r dx$
On en déduit :
$\pi r^2 P_e – \pi r^2 P_s $$+ \eta \frac{d v(r)}{dr} 2 \pi r dx= 0$
Ce qui permet d’isoler la dérivée :
$\frac{dv(r)}{dr} = – \frac{P_e – P_s}{2 \eta dx} r$ $=\frac{dp}{2 \eta dx}r$
On intègre par rapport au rayon (dans ce cas dp/dx est constant) et on obtient :
$v(r)= \frac{dp}{2 \eta dx} \frac{r^2}{2}+cte$
La constante est obtenue connaissant v(r=R)=0.
$v(R)= 0=\frac{dp}{2 \eta dx} \frac{R^2}{2}+cte$ $\Rightarrow$ $cte = – \frac{dp}{2 \eta dx} \frac{R^2}{2}$
Soit :
$v(M)= \frac{dp}{2 \eta dx} \frac{(r^2 – R^2)}{2}$
29. En déduire l’expression du débit de volume $𝑄$ en fonction de $𝑅, 𝜂 et \frac{d𝑝}{d𝑥}$.
On ne peut pas utiliser la formule $Q=v \times S$ car la vitesse n’est pas constante sur la surface. Il faut alors revenir à la formule locale :
$Q=\iint _S \vec v (M) \vec{dS}$ avec $dS=r d \theta dr$
Soit : $Q=\iint _S v (M) r d \theta dr$ $=\iint _S \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r d \theta dr$ $=\int_{0}^{2 \pi} d \theta \int_{0}^{R} \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r dr$ $=2\pi \int_{0}^{R} \frac{r^2 – R^2}{4 \eta} \frac{dp}{dx} r dr$ $=\frac{2 \pi}{4 \eta} \frac{dp}{dx} \int_{0}^{R} (r^3 -R^2 r)dr$ $=\frac{ \pi}{2 \eta} \frac{dp}{dx} [(\frac{r^4}{4} – R^2\frac{r^2}{2})]_{0}^{R} $ $=\frac{ \pi}{2 \eta} \frac{dp}{dx} [\frac{R^4}{4} – \frac{R^4}{2}]$ $= – \frac{\pi R^4}{8 \eta} \frac{dp}{dx}$
30. En déduire la dimension de la viscosité dynamique 𝜂 en fonction des dimensions fondamentales suivantes : longueur, masse et temps.
On a $\eta \# \frac{R^4 }{Q } \frac{dp}{dr}$ $= \frac{[L]^4}{\frac{[L]^3}{[T]}} \frac{[M].[L]^{-1}.[T]^{-2}}{[L]}$ $=\frac{[M]}{[L].[T]}$
II. Modélisation de l’écoulement de la Mer de glace
On choisit de modéliser l’écoulement de la Mer de glace par l’écoulement de Poiseuille stationnaire d’un fluide visqueux newtonien incompressible s’écoulant dans la moitié inférieure d’une conduite cylindrique sous le seul effet de la gravité, ce qui impose de remplacer dans l’expression (1) de la vitesse d’écoulement $\frac{dp}{dx}$ par $−𝜌_𝑔 𝑔 sin 𝛼$, où $𝜌_𝑔$ est la masse volumique de la glace, $𝑔$ la norme de l’accélération de la pesanteur et $𝛼$ l’angle qui mesure la pente moyenne de la Mer de glace.
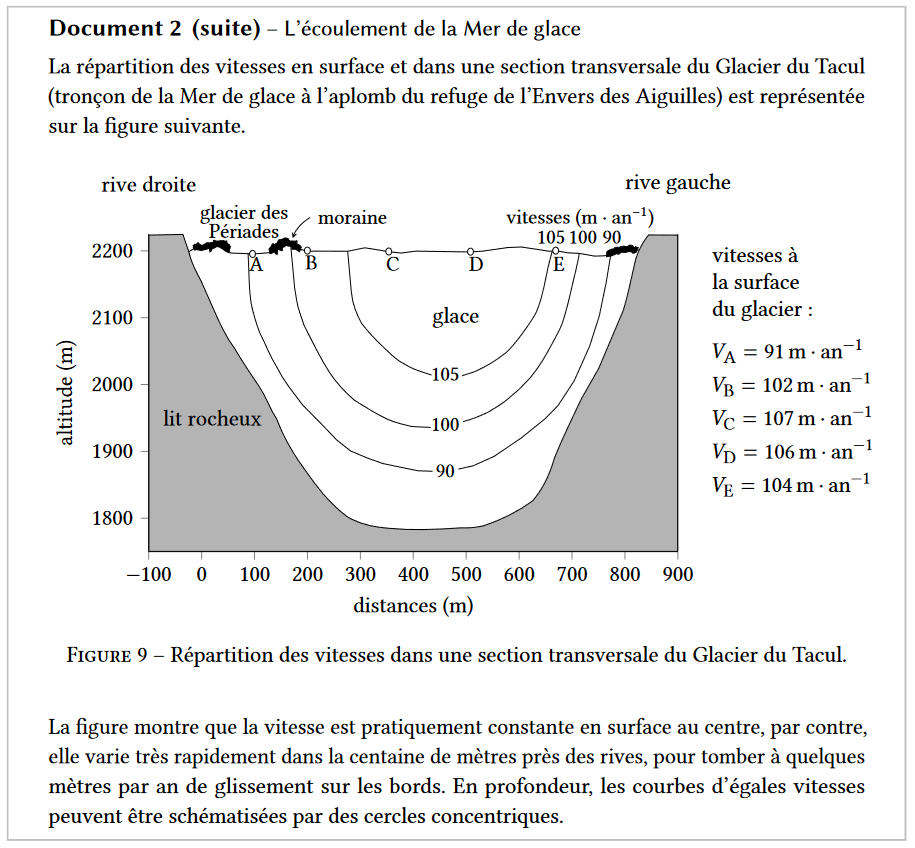
31. À partir d’une analyse de la figure 9, proposer au moins un argument en faveur et au moins un argument en défaveur de ce choix de modélisation de l’écoulement du glacier par un écoulement de Poiseuille.
Argument en faveur : On observe bien une diminution de la vitesse lorsque l’on s’éloigne du centre en surface caractéristique d’un écoulement de Poiseuille. Que ce soit sur les bords ou en profondeur.
Argument en défaveur : La forte diminution de la vitesse sur les 100 derniers mètres ne sont pas compatibles avec un écoulement de Poiseuille.
32. En utilisant les données quantitatives disponibles dans le document 2 et en particulier sur la figure 9, proposer une estimation de l’ordre de grandeur de la viscosité dynamique de la glace. Comparer l’ordre de grandeur obtenu avec la valeur estimée usuelle de la viscosité de la glace de l’ordre de $10^{13} Pa⋅s$. Commenter.
D’après la formule (1) on a : $v(M)= \frac{(r^2 – R^2)}{4 \eta} (- \rho _g g sin \alpha)$ soit $\eta= \frac{(r^2 – R^2)}{4 v(M)} (- \rho _g g sin \alpha)$
Pour le calcul on prends le point E ($v_E$ est donné) on le situe à 200m du centre en surface.
Application Numérique :
$\eta= \frac{(200^2 – 400^2)}{4 \frac{104}{365\times 24 \times 3600}} (- 917 \times 9,81 sin 11)$ $=1,56.10^{13} Pa.s$
Malgré la non symétrie du profile des vitesses, on retrouve une valeur de la viscosité dynamique très proche de la valeur usuelle.