Physique BCPST
Mécanique des fluides | Poiseuille
Extrait du sujet 2024 AGRO-VETO voir le sujet corrigé complet
On donne le lien entre le mmHg et le bar : 760 mmHg = 1,013 bar.
C. Exploitation des mesures de pression artérielle systémique.
Dans toute cette sous-partie C, toutes les valeurs de pression artérielle correspondent à la pression
différentielle $Δ𝑃 = 𝑃 − 𝑃_{atm}$. Par exemple, une pression artérielle de $120 mmHg$ correspond à une pression absolue de $760 mmHg + 120 mmHg = 840 mmHg$. De plus, toutes les mesures sont prises pour un individu allongé et au repos.
II. Introduction à l’hémodynamique
L’hémodynamique (ou « dynamique du sang ») est la science des propriétés physiques de la circulation sanguine en mouvement dans le système cardiovasculaire.
On propose dans cette partie d’étudier de manière simplifiée quelques aspects de l’hémodynamique.
Dans toute cette partie II l’individu est allongé et au repos.
A. Écoulement dans un vaisseau sanguin
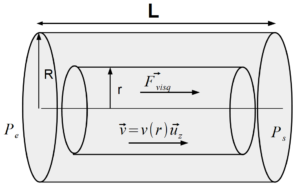
On s’intéresse d’abord à l’écoulement horizontal du sang dans un seul vaisseau sanguin qu’on assimile à une conduite cylindrique indéformable de diamètre $𝑑$ et de longueur $𝐿$ (voir figure 6 ci-dessous).
Le sang est un fluide incompressible de masse volumique $𝜌_s = 1 060 kg.m^{−3}$. De plus, dans un souci de simplicité, on considérera que le sang est un fluide newtonien de viscosité dynamique égale à $𝜂_s = 1,6 × 10^{−3} Pa.s $.
L’écoulement du sang est supposé stationnaire et laminaire.
Le gradient de pression est uniforme le long de la conduite et on note $Δ𝑃 = 𝑃(𝑥 = 0) − 𝑃(𝑥 = 𝐿) > 0$ la différence de pression entre le début et la fin du vaisseau sanguin considéré.
Le champ des vitesses est de la forme $\vec{𝑣} = 𝑣(𝑟) \vec{u_x}$ en coordonnées cylindriques d’axe $(𝑂𝑥)$.
Enfin, la force de viscosité que le sang à l’extérieur du cylindre de rayon $𝑟 ≤ \frac{𝑑}{2}$, d’axe $(𝑂𝑥)$ et de longueur $𝐿$ exerce sur le sang situé à l’intérieur de ce cylindre s’écrit : $\vec{𝐹_{visc}} = 2𝜋𝑟𝐿𝜂_s \frac{d𝑣(𝑟)}{d𝑟} \vec{𝑢_𝑥}$ .
11. À partir d’un bilan de quantité de mouvement sur un système à expliciter, montrer que la vitesse du fluide s’exprime selon : $\vec{𝑣} = \frac{Δ𝑃}{4𝜂_s 𝐿} (\frac{𝑑^2}{4} − 𝑟^2) \vec{𝑢_𝑥}$ .
Cette démonstration fait partie des démonstrations à savoir refaire comme indiqué dans le Bulletin Officiel (BO).
On étudie l’écoulement unidimensionnel d’un fluide visqueux dans un cylindre horizontal de rayon R et de longueur L, en régime stationnaire (indépendant du temps). On suppose un écoulement laminaire (Re<2000). on néglige la pesanteur.
On considère une portion dufluide cylindrique, de rayon r et de longueur L.
Il existe une pression en entrée différente de la pression en sortie ce qui permet le déplacement du fluide.
En régime stationnaire, la variation de quantité de mouvement est nulle, soit : $\sum \vec{F} = \frac{d \vec p}{dt} = 0$
Les forces qui s’appliquent sur le volume de fluide sont les forces pressentes en entrée et en sortie ainsi que la force visqueuse due au sang à l’extérieur. Le poids est négligé.
$\vec{F_{pe}} – \vec{F_{ps}} + \vec {F_{visq}} = 0$
$P_{e} S \vec{u_x} – P_{s} S \vec{u_x} + 2 \pi r L \eta_S \frac{d v(r)}{dr} \vec {u_x} = 0$
$P_{e} \pi r^2 – P_{s} \pi r^2 + 2 \pi r L \eta_S \frac{d v(r)}{dr} = 0$
Soit : $\frac{dv(r)}{dr}= – \frac{\Delta P r}{2 L \eta_S}$
On intègre alors entre un rayon r et le rayon R (ici on choisi les bornes d’intégration entre r et R car la vitesse en R est nulle v(r=R)=0 et la borne r nous permettra d’avoir la vitesse v(r))
$\int _{v(r)}^{v(r=R)}\frac{dv(r)}{dr}= – \int _r^R \frac{\Delta P r}{2 L \eta_S}$
$[v]_{v(r)}^{v(r=R)} = – \frac{\Delta P }{2 L \eta_S} [\frac{r^2}{2}]_r^R$
$0-v(r) = – \frac{\Delta P }{2 L \eta_S} [\frac{R^2 – r^2}{2}]$
Soit : $v(r) = \frac{\Delta P }{4 L \eta_S} [\frac{d^2}{4} – r^2]$
Représenter ensuite le champ des vitesses dans une section droite de conduite.
12. En déduire l’expression du débit de volume $𝐷_𝑉$ en fonction des données de l’énoncé
Le débit volumique $D_V = \iint _S v dS$ $=\iint _S \frac{\Delta P}{4 \eta _S L}(\frac{d^2}{4} – r^2)dS$
Or $dS = rd \theta dr$ et $\frac{d^2}{4} = R^2$
On a alors : $D_V=\int _0^{2\pi} d\theta \int_0^R \frac{\Delta P}{4 \eta _S L}(R^2 – r^2)rdr$ $=2\pi \frac{\Delta P}{4 \eta _S L } \int_0^R (R^2 – r^2)rdr$ $=\pi \frac{\Delta P}{2 \eta _S L } \int_0^R (R^2 r – r^3)dr$ $=\pi \frac{\Delta P}{2 \eta _S L } [(\frac{R^2 r^2}{2} – \frac{r^4}{4})]_0^R $ $=\pi \frac{\Delta P}{2 \eta _S L } [(\frac{R^4 }{2} – \frac{R^4}{4})]$ $=\pi \frac{\Delta P R^4}{8 \eta _S L }$
13. On définit la résistance hydraulique de sorte que $Δ𝑃 = 𝑅_h 𝐷_𝑉$. Montrer que la résistance hydraulique s’exprime sous la forme : $𝑅_h = \frac{128𝜂_s𝐿}{𝜋𝑑^4}$ .
$Δ𝑃 = 𝑅_h 𝐷_𝑉$ donc : $R_h = \frac{\Delta P}{𝐷_𝑉}$ $=\frac{\Delta P 8 \eta _S L}{\Delta P \pi R^4}$ $=\frac{8 \eta _S L}{\pi R^4}$ $=\frac{128 \eta _S L}{\pi d^4}$
Dans la suite du sujet, la relation $Δ𝑃 = 𝑅_h 𝐷_𝑉$ avec $𝑅_h = \frac{128𝜂_s 𝐿}{𝜋𝑑^4}$ constitue la loi de Poiseuille.
B. Prise en compte de l’ensemble des vaisseaux sanguins.
On souhaite prendre en compte l’ensemble des vaisseaux sanguins de la circulation systémique pour estimer la perte de charge entre la sortie du cœur gauche et l’entrée du cœur droit.
On se propose de calculer la perte de charge due aux artérioles afin d’effectuer une comparaison avec les données réelles. On supposera que la loi de Poiseuille peut s’appliquer dans tous les vaisseaux sanguins.
14. À partir du tableau 1, déterminer le débit de volume du sang dans l’aorte $𝐷_𝑉$.
Justifier ensuite que le nombre d’artérioles dans le corps humain vaut environ $𝑁_{artérioles} ≃ 1,5 × 10^6$.
Le piège ici est de partir de la formule du débit volumique trouvée question 12 en prenant la pression dans l’aorte comme étant $\Delta P$. Or $\Delta P$ représente la variation de pression entre l’entrée et la sortie de l’aorte (information que l’on a pas!)
On doit repartir de la formule du débit volumique liant vitesse et section : $D_V = vS$ $=\frac{v \pi d^2}{4}$
AN : $D_V = \frac{2,65.10^{-1} \pi (20.10^{-3})^2}{4} = 8,32.10^{-5} m^3 . s^{-1}$ , soit $D_V=8,32cL.s^{-1}$
Pour trouver le nombre d’artérioles, il faut garder en tête que le débit volumique est conservatif, de plus les artérioles sont mis en dérivation donc $D_{V,aorte}= N_{artérioles} \times D_{V,artérioles}$
On retrouve le débit volumique d’une artériole en utilisant la formule définie à la question précédente :
$D_{V,artérioles}=\frac{v \pi d^2}{4} $
AN :
$D_{V,artérioles}=\frac{2,80.10^{-2} \pi (0,05.10^{-3})^2}{4}=5,5.10^{-11} m^3 .s^{-1} $
Au final :
$ N_{artérioles} = \frac{D_{V,aorte}}{D_{V,artérioles}}$
AN :
$ N_{artérioles} = \frac{8,32.10^{-5}}{5,5.10^{-11}} \simeq 1,5.10^6$
15. En prenant $𝐷_𝑉 = 5,0 L.min^{−1}$, estimer les pertes de charge $Δ𝑃_{artérioles}$ dans les artérioles. Comparer cette valeur à celle pouvant être déterminée à partir du tableau 1. Commenter et proposer une brève explication aux écarts observés entre les deux valeurs.
$\Delta P = R_h D_V = \frac{128 \eta _S L}{\pi d^4} D_V$
AN :
$\Delta P = \frac{128 1,6.10^{-3}.10.10^{-3}}{\pi (0,05.10^{-3})^4} \frac{5.10^{-3}}{60} = 5794Pa$
D’après le tableau 1. La pression en entrée d’artériole est de 86 mmHg et en sortie 30mmHG (équivalent à la pression en entrée de capillaires) soit une différence de 56mmHg équivalent à une différence de pression de 7464Pa
La différence peut provenir de l’approximation faite sur le débit volumique.