Physique BCPST
CIRCUITS | Grandeurs électriques
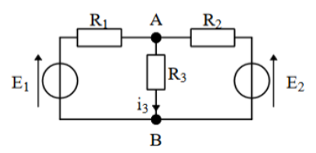
Exercice 1 : Loi des noeuds, loi des mailles
Exprimer $i_3$, en fonction de $E_1$, $E_2$, $R_1$, $R_2$, et $R_3$.
1) Exprimer $i_3$, en fonction de $E_1$, $E_2$, $R_1$, $R_2$, et $R_3$.
Réponse
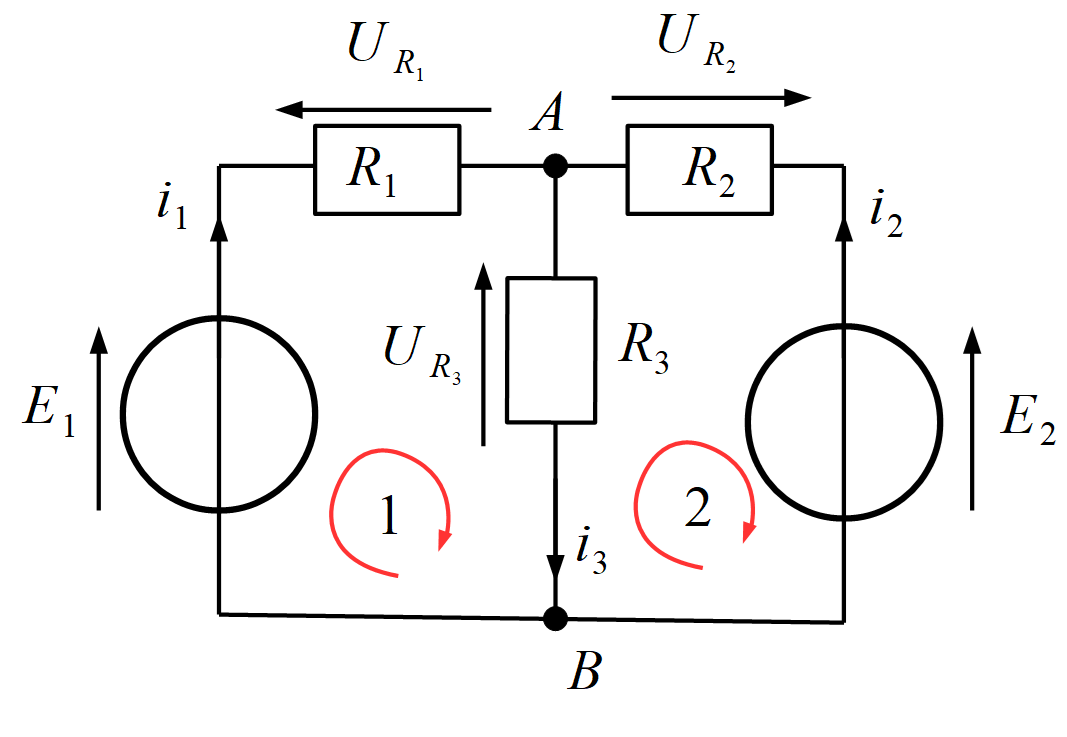
Il faut avant tout compléter le schéma avec les différents courants et les tensions (attention aux conventions récepteurs). On peut également ajouter les 2 mailles et le sens d’utilisation.
$i_3=i_1 + i_2$
Loi des mailles :
1 : $E_1 – U_{R_1} – U_{R_3} = 0$
2 : $U_{R_3} + U_{R_2} – E_2 = 0$
Les lois des mailles se réécrivent :
1 : $E_1 – R_1 i_1 – R_3 i_3 = 0$ $\Rightarrow$ $i_1 = \frac{E_1 – R_3 i_3 }{R_1}$
2 : $R_3 i_3 + R_2 i_2 – E_2 = 0$ $\Rightarrow$ $i_2 = \frac{E_2 – R_3 i_3 }{R_2}$
En injectant les courants dans la loi de nœuds, on obtient :
$i_3=i_1 + i_2 = \frac{E_1 – R_3 i_3 }{R_1} + \frac{E_2 – R_3 i_3 }{R_2}$
$\Rightarrow$ $i_3 + \frac{R_3 i_3}{R_1} + \frac{R_3 i_3}{R_2} = \frac{E_1}{R_1} + \frac{E_2}{R_2}$ $\Rightarrow$ $i_3 (1 + \frac{R_3}{R_1} + \frac{R_3}{R_2}) = \frac{E_1}{R_1} + \frac{E_2}{R_2}$ $\Rightarrow$ $i_3 = \frac{\frac{E_1}{R_1} + \frac{E_2}{R_2}}{1 + \frac{R_3}{R_1} + \frac{R_3}{R_2}}$
2) Application Numérique avec $E_1 = 10 V$ ; $E_2 = 5 V$. $R_1 = 15 Ω$ ; $R_2 = 10 Ω$ et $R_3 = 5 Ω$
Réponse
$i_3 = \frac{\frac{10}{15} + \frac{5}{10}}{1 + \frac{5}{15} + \frac{5}{10}} = \frac{7}{11} = 0,64A$