Physique BCPST
OPTIQUE | Lois de Snell-Descartes
Exercice 1 : Dispersion par le verre
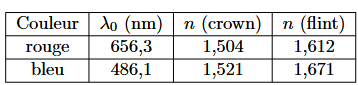
Le tableau ci-contre donne les longueurs d’onde, dans le vide, de deux radiations monochromatiques et les indices correspondants pour deux types de verre différents.
1) Calculer les fréquences de ces ondes lumineuses. Dépendent-elles de l’indice du milieu ? On prendra $c_0 = 2, 998.10^8 m.s^{−1}$.
Réponse
Les fréquences ne dépendent pas de l’indice du milieu, uniquement la vitesse de propagation et la longueur d’onde.
-$f_{rouge} = \frac{c_0}{\lambda}$
Application Numérique :
$f_{rouge} = \frac{2,998.10^8}{656,3.10^{-9}}= 457 THz$
-$f_{bleu} = \frac{c_0}{\lambda}$
Application Numérique :
$f_{bleu} = \frac{2,998.10^8}{486,1.10^{-9}}= 617 THz$
2) Calculer les célérités et les longueurs d’onde de la radiation rouge dans les deux verres.
Réponse
$v=\frac{c_0}{n}$
$\lambda=\frac{v}{f}$
Application Numérique :
– Dans le crown :
$v=\frac{2,998.10^8}{1,504}= 1,993.10^8 m.s^{-1}$
$\lambda=\frac{1,993.10^8}{457.10^12} = 436 nm$
– Dans le flint :
$v=\frac{2,998.10^8}{1,612}= 1,860.10^8 m.s^{-1}$
$\lambda=\frac{1,860.10^8}{457.10^12} = 407 nm$
3) a) Un rayon de lumière blanche arrive sur un dioptre plan air-verre, sous l’incidence $i = 60°$. L’indice de l’air est pris égal à 1, 000. Rappeler les lois de Descartes relatives à la réfraction de la lumière.
Réponse
Loi de Snell-Descartes de la réfraction :
Le rayon réfracté est dans le même plan que le rayon incident et la normale au dioptre.
on a : $n_1 sin i = n_2 sin r$ avec $n_1$ l’indice de réfraction du milieu traversé par le rayon incident, $n_2$ l’indice de réfraction du milieu traversé par le rayon réfracté, $i$ angle entre la normale et le rayon incident, $r$ angle entre la normale et le rayon réfracté.
b) Calculer l’angle que fait le rayon bleu avec le rayon rouge pour un verre crown, puis pour un verre flint.
Réponse
Pour retrouver l’angle entre le rayon bleu et le rouge, il faut faire la différence entre les angles de réfraction pour la couleur bleue et rouge.
-Dans le verre crown
$\alpha = r_{bleu} – r_{rouge} = arcsin(\frac{n_1 sin i}{n_{b,crown}}) – arcsin(\frac{n_1 sin i}{n_{r,crown}})$
Application Numérique :
$\alpha = arcsin(\frac{1,000 \times sin (60°)}{1,521}) – arcsin(\frac{1,000 \times sin (60°)}{1,504}) = – 0,450° $
Les deux rayons ont un écart angulaire de 0,450 degré dans le verre crown
-Dans le verre flint
$\alpha = r_{bleu} – r_{rouge} = arcsin(\frac{n_1 sin i}{n_{b,flint}) – arcsin(\frac{n_1 sin i}{n_{r,flint})$
Application Numérique :
$\alpha = arcsin(\frac{1,000 \times sin (60°)}{1,671}) – arcsin(\frac{1,000 \times sin (60°)}{1,612}) = – 1,280° $
Les deux rayons ont un écart angulaire de 1,280 degré dans le verre flint
c) Quel est le verre le plus dispersif ?
Réponse
Le verre le plus dispersif est le flint car l’écart angulaire entre les rayons de différentes couleurs est le plus grand.