Physique BCPST2
Mécanique des fluides | Poussée d'Archimède
Extrait du sujet 2023 A BCPST voir le sujet corrigé complet
2. La fonte des inlandsis
Un inlandsis est un glacier de grande étendue qui se présente sous la forme d’une couche de glace dont l’épaisseur peut atteindre plusieurs milliers de mètres et qui recouvre le sol. Il n’existe sur Terre que deux inlandsis : celui du Groënland et celui de l’Antarctique. Ces deux inlandsis se prolongent vers la mer ou l’océan sous la forme de barrières de glace, dont se détachent les icebergs.
On propose d’abord dans cette partie d’estimer la hausse du niveau des océans sur Terre qui résulte de la fonte des inlandsis ou de la fonte des icebergs. Dans la dernière sous-partie est abordé l’aspect énergétique de la fusion de la glace, tel qu’il peut être étudié en séance de travaux pratiques.
I. Équilibre hydrostatique d’un glaçon dans l’eau liquide
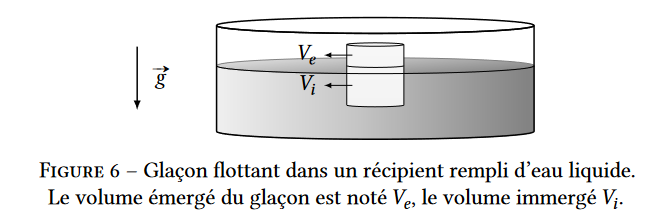
Afin d’analyser l’éventuel impact de la fonte des icebergs sur l’élévation du niveau des océans, on propose d’étudier une situation modèle. On considère l’équilibre d’un glaçon, constitué d’eau pure, dans un récipient contenant de l’eau liquide (voir figure 6).
14. Donner l’expression de la poussée d’Archimède $\vec Π$ que l’eau liquide exerce sur le glaçon en fonction du volume immergé $𝑉_𝑖$, de la masse volumique $𝜌_ℓ$ de l’eau liquide et de l’accélération de la pesanteur $\vec 𝑔$ .
$\vec \Pi = – \rho_l V_i \vec g$
15. Rappeler la nature des actions mécaniques à l’origine de la poussée d’Archimède.
Les actions mécaniques à l’origine de la poussée d’Archimède sont les forces pressantes exercées par l’eau sur la face inférieure du glaçon et plus précisément la différence de force pressante entre le haut de l’objet immergé et le bas.
16. On fait l’hypothèse que la poussée d’Archimède exercée par l’air est négligeable devant celle exercée par l’eau. Préciser néanmoins le sens de la poussée d’Archimède exercée par l’air sur le glaçon.
L’air exerce une pression sur la partie latérale du glaçon qui se compense de chaque coté et donc s’annule.
L’air exerce également une force pressante sur le dessus du glaçon qui n’est pas compensé. On a donc une poussée exercée par l’air sur le glaçon orienté vers le bas.
17. Exprimer le volume émergé $𝑉_𝑒$ en fonction du volume immergé $𝑉_𝑖$ et des masses volumiques de l’eau liquide $𝜌_ℓ$ et de la glace $𝜌_𝑔$.
On applique le principe fondamental de la dynamique : $\sum \vec F = m \vec a = \vec 0$
$\vec P + \vec \Pi = \vec 0$ $\Rightarrow$ $m \vec g – \rho_l V_i \vec g = \vec 0$
$m=\rho_l V_i$, or $m=\rho_g V_{tot}$ avec $V_{tot}= V_i + V_e$
$\Rightarrow$ $\rho_l V_i = \rho_g (V_e + V_i)$ $\Rightarrow$ $V_e=V_i[\frac{\rho_l}{\rho_g}-1]$
On repère le niveau de l’eau liquide dans le récipient juste après avoir déposé le glaçon et juste après la fonte de celui-ci.
18. Justifier que le niveau d’eau liquide dans le récipient ne varie pas après la fonte du glaçon.
Ici il faut démontrer que le volume qu’occuperait l’eau issue de la totalité de la fonte du glaçon $V_{l,fus}$ correspond au volume $V_i$ occupé par le glaçon.
$V_{l,fus}= \frac{m_g}{\rho_l}$ $=\frac{\rho_g V_{tot}}{\rho_l}$ $=\frac{\rho_g (V_i + V_e)}{\rho_l}$ or $V_e=V_i[\frac{\rho_l}{\rho_g}-1]$ (q.17) donc :
$=\frac{\rho_g (V_i + V_i[\frac{\rho_l}{\rho_g}-1])}{\rho_l}$ $=\frac{\rho_g}{\rho_l} \times \frac{\rho_l}{\rho_g} \times V_i $ $= V_i$
19. Préciser si ce résultat se maintient dans le cas où le glaçon constitué d’eau pure flotte dans de l’eau salée, de masse volumique supérieure à celle de l’eau pure.
On a le même glaçon donc la même masse et le même volume d’eau lorsqu’il a fondu. Or comme il était plongé dans un milieu plus dense, le volume immergé est plus petit car le produit $\rho_l \times V_i$ reste constant.
On a donc une montée de l’eau lors de la fonte de la glace d’eau pure dans une eau salée.
20. Conclure quant à l’éventuelle contribution de la fonte des icebergs à l’élévation du niveau des océans.
Les icebergs sont constitués d’eau douce et flottent dans de l’eau salée, on se retrouve dans la même configuration que la question précédente. Lorsque l’iceberg fond il fait augmenter le niveau des océans.
II. Hausse du niveau des océans due à la fonte des inlandsis.
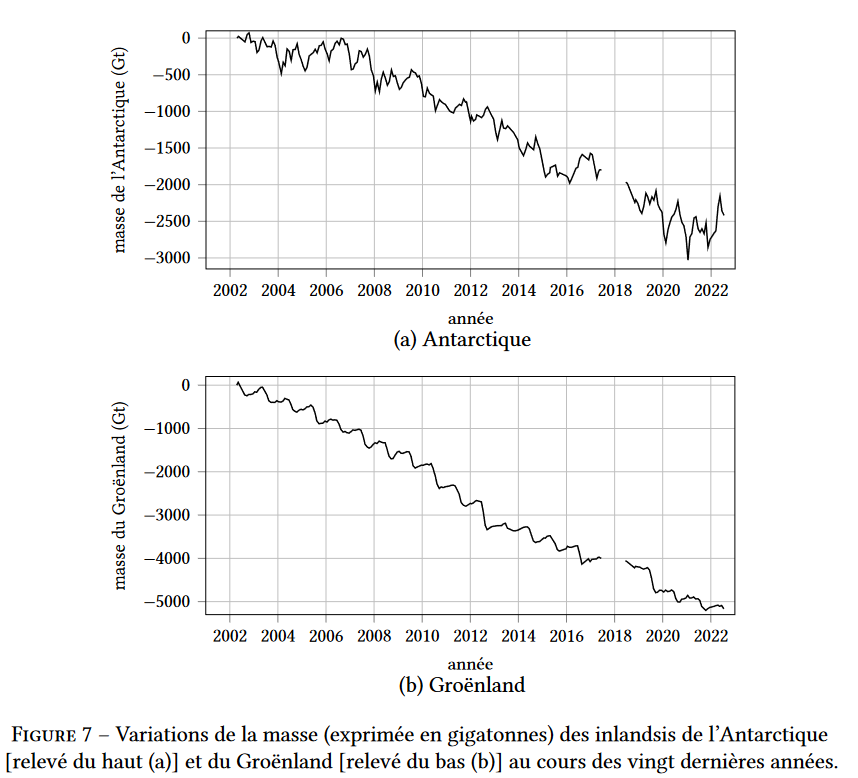
La fonte de la glace qui constitue les inlandsis contribue à l’élévation du niveau des océans. Les variations de l’épaisseur moyenne des inlandsis se déduisent des mesures de leur altitude de surface par des satellites dédiés. La figure 7 représente les variations estimées de la masse des inlandsis de l’Antarctique et du Groënland depuis 2002.
21. Les relevés de la figure 7 présentent des oscillations particulièrement visibles dans le cas du Groënland (graphique (b) à droite de la figure). Estimer grossièrement la période de ces oscillations et proposer une interprétation de leur origine.
On observe 2 oscillations par an soit une période de 6 mois. Cela est du aux périodes hiver/été. L’hiver la glace se reforme et l’été elle fond.
22. Estimer la hausse du niveau des océans consécutive à la fonte des inlandsis du Groënland et de l’Antarctique pendant les vingt dernières années, en s’appuyant sur les données de la figure 7.
Sur la figure a) on perd environ $2700 Gt$ de glace et sur la figure b) on perd $5100Gt$ de glace soit au total 7800Gt.
La masse perdue est de $m=7,8.10^{15}kg$, ce qui correspond à un volume de $V=\frac{m}{\rho_g}$ $=8,5.10^{12}m^3$
Calcul de la surface de la Terre :
$S_{terre}=4 \pi R_t^2$ $=5,15.10^{14}m^2$
On retrouve la hauteur en considérant que l’eau recouvre 70% de la surface de la Terre correspondant aux océans.
$V =\frac{70}{100} \times S_{Terre} \times h$ $\Rightarrow$ $h=\frac{V}{\frac{70}{100} S_{Terre}}$ $=23,6cm$ soit 1,2cm/an.