Physique BCPST
Mécanique des fluides | Principe hydrostatique
Extrait du sujet 2024 A BCPST (voir le sujet corrigé complet)
L’APPAREIL CARDIOVASCULAIRE
Introduction.
L’appareil cardiovasculaire est un système circulatoire en circuit fermé qui assure le transport du sang. Il est constitué du cœur et des vaisseaux sanguins.
On distingue la circulation systémique et la circulation pulmonaire :
— la circulation systémique amène le sang chargé en dioxygène (noté $O_2$ dans la suite du sujet) depuis le cœur gauche jusqu’aux organes puis ramène ce même sang déchargé en $O_2$ mais chargé en dioxyde de carbone (noté $CO_2$ dans la suite du sujet) jusqu’au cœur droit.
— la circulation pulmonaire amène ensuite le sang veineux (sang déchargé en $O_2$ et chargé en $CO_2$) au contact des alvéoles pulmonaires pour le ré-oxygéner puis renvoie ce sang au cœur gauche via la veine pulmonaire.
I. La pression artérielle.
Dans cette partie, on s’intéresse à la mesure de la pression artérielle. Après avoir établi le lien entre le millimètre de mercure (noté mmHg) et le bar (sous-partie A), un dispositif de mesure de pression est présenté (sous-partie B). Enfin, des données de pression artérielle (sous-partie C) sont étudiées.
A. À propos du millimètre de mercure.
En médecine, l’unité encore largement utilisée pour exprimer les pressions est le millimètre de mercure.
On se propose d’établir le lien entre le mmHg et le bar : 760 mmHg = 1,013 bar.
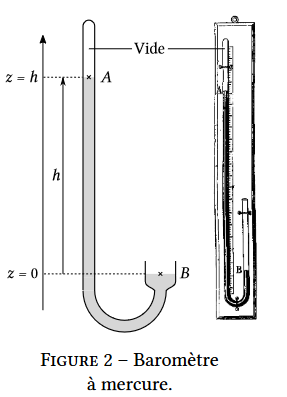
Pour cela, on considère le baromètre à siphon représenté ci-après sur la figure 2.
Ce baromètre utilise du mercure liquide, fluide incompressible de masse volumique $𝜌_Hg = 13,6 × 10^3 kg.m^{−3}$. On note $𝑃_atm = 1,013 bar$ la pression atmosphérique et $𝑔 = 9,81 m⋅s^{−2}$ l’accélération de la pesanteur.
Le point 𝐵 est en contact avec l’atmosphère de sorte que $𝑃_𝐵 = 𝑃_atm$.
On néglige tout phénomène de tension superficielle. De plus, comme la pression de vapeur saturante du mercure est très faible devant la pression atmosphérique, on assimilera l’espace au dessus du point 𝐴 à du vide ; en particulier on considérera que $𝑃_𝐴 ≃ 0 bar$.
1. Rappeler puis établir la relation fondamentale de la statique des fluides dans un fluide de masse volumique $𝜌$ pour un axe $𝑧$ vertical ascendant. Pour la démonstration on pourra postuler que la pression $𝑃$ ne dépend que de la variable $𝑧$, puis écrire l’équilibre d’une couche de fluide comprise entre $𝑧$ et $𝑧 + d𝑧$.
Relation fondamentale de la statique des fluides : $dP = – \rho g dz$ pour un axe z vertical ascendant.
Démonstration :
Soit une couche de fluide comprise entre $z$ et $z +dz$
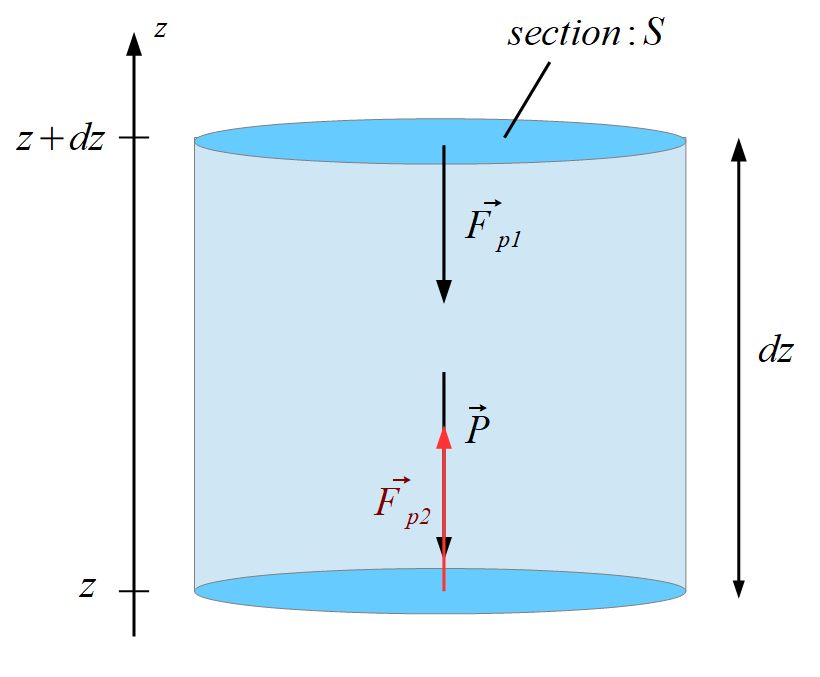
Système d’étude : {couche de fluide élémentaire}
Référentiel terrestre supposé galiléen
2ème loi de Newton :
$\sum \vec F = m \vec a = \vec 0$ car le système est à l’équilibre.
$\Rightarrow$ $\vec P + \vec F_{P1} + \vec F_{P2} = \vec 0$
On projète sur l’axe (Oz) :
$-dm g – F_{P1} + F_{P2} = 0$ $\Rightarrow$ $-P(z+dz) \times S + P(z) \times S = dm g = \rho dV g = \rho dz S g$ $\Rightarrow$ $P(z+dz) – P(z) = dP = – \rho g dz$
2. Établir l’expression de 𝑃(𝑧) dans le mercure liquide.
Dans le mercure : $dP = P(z) – P_A = – \rho_{Hg} g (z – z_A)$ $\Rightarrow$ $P(z) = P_A -\rho_{Hg} g (z – h) = P_A +\rho_{Hg} g ( h-z) $
3. Montrer que la hauteur $ℎ$ de liquide entre les points $𝐴$ et $𝐵$ s’exprime selon $ℎ = \frac{𝑃_{atm}}{𝜌_{Hg}𝑔}.$ Faire l’application numérique de $ℎ$ puis commenter le résultat.
Appliquons le principe de l’hydrostatique entre les points A et B :
$P_A – P_B = – \rho_{Hg} g (z_A – z_B)}$ , ici nous avons $P_A \simeq 0$ et $P_B = P_{atm}$ on obtient alors :
$- P_{atm} = – \rho_{Hg} g h$ $\Rightarrow$ $h= \frac{P_{atm}}{\rho_{Hg}g}$
4. Justifier l’utilisation du mercure plutôt que de l’eau liquide pour la réalisation d’un baromètre à siphon.
La hauteur $h$ est inversement proportionnelle à la masse volumique du liquide dans le baromètre. Or la masse volumique de l’eau est environ 14 fois plus faible que celle du mercure. Pour une même variation de pression on aurait alors une différence de hauteur 14 fois plus grande. Au final il faudrait fabriquer un baromètre 14 fois plus grand.
5. Expliquer qualitativement pourquoi les tubes du baromètre ne doivent pas être « trop fins » pour que l’étude précédente soit valable.
Si les tubes étaient plus fins, le liquide à l’intérieur subirait une force de capillarité plus grande. Il faudrait alors prendre en compte cette force dans le bilan des forces ce qui compliquerait le raisonnement.


