Utilisation de la loi de Jurin : Physique BCPST2
ÉNONCÉ
Quand on plonge verticalement, un tube capillaire de rayon r, dans un liquide de masse volumique $\rho_0$, dont la constante de tension superficielle est $\gamma$, à température constante, on observe une ascension capillaire du liquide, de hauteur h.
$h = \frac{2 \gamma}{r \rho_{0}g}$
Question 1 : Unité de la tension superficielle
Montrer que $\gamma$ peut s’exprimer en $N.m^{-1}$
Effectuer une analyse dimensionnelle pour retrouver l’unité.
2 : Analyse graphique
On plonge 4 tubes capillaires de diamètre différents dans le même liquide et on mesure pour chacun la hauteur h. On a trouvé les résultats suivants :
Question 2.1 : Vérification graphique
Montrer par un graphique approprié que cette expérience vérifie la loi de Jurin.
Représenter h en fonction de 1/r . Attention aux unités
Question 2.2 : Retrouver $\gamma$
Déduire la constante de tension superficielle $\gamma$ à la température de l’expérience sachant que $\rho_{0} = 1000kg.m^{-3}$
Retrouver la constante à partir de la pente de la courbe.
CORRIGÉ
Question 1
Pour montrer que $\gamma$ s’exprime en $N.m^{-1}$ il faut effectuer une analyse dimensionnelle de $\gamma$
soit : $\gamma = \frac{h r \rho_{0}g}{2}=[L] \times [L] \times \frac{[M]}{[L]^3} \times \frac{[L]}{[T]^2}$ $= \frac{[M]}{[T]^2} = \frac{N}{m}$
Question 2.1
On représente h en fonction de 1/r car dans ce cas on représente h =f(1/r) qui correspond à la formule $h = \frac{2 \gamma}{ \rho_{0}g} \times \frac{1}{r}$ ce qui revient à étudier une fonction affine y=ax
Question 2.2
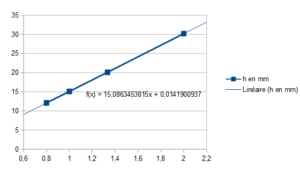
A partir de la courbe précédente on retrouve un coefficient directeur de 15,08 en convertissant les mm en m. on retrouve $15,08.10^{-6}$
Ce coefficient directeur correspond à $ \frac{2 \gamma}{ \rho_{0}g}$
Soit $ \gamma = \frac{\rho_{0}g \times 15,08.10^{-6}}{ 2} = 7,54.10^{-2} N/m $
