Thermodynamique
Entropie | Second principe
énergie absorbée : $\Delta H = mc \Delta T$
EXERCICE 1
On chauffe 1g de glace initialement à la température $T_i = -18°C$ pour la transformer en eau liquide à une température de $T_2 = 20°C$ à pression atmosphérique.
Données : Enthalpie de fusion de l’eau à 0°C : $\Delta_{fus} H = 333J.g^{-1}$ ; Capacités thermiques massique de l’eau :$c_e=4,15 kJ.K^{-1}.kg^{-1}$, de la glace : $c_g=2,10 kJ.K^{-1}.kg^{-1}$ .
Question 1 : Enthalpie
1) Déterminer la variation d’enthalpie de l’eau.
Réponse
$\Delta H = \Delta H_{glace} + \Delta H_{glace->eau}$ $+ \Delta H_{eau-liquide}$ $= m_g c_g (0°C – T_g)$ $+ m_g \Delta _{fus} h$ $+m_g c_e(T_f – 0°c) $ $=10^{-3}. 2,10.10^3 (0 – (-18)) +333 $$ + 10^{-3}. 4,15.10^3 .(20)$ $=453,8J$
Question 2 : Entropie
2) Déterminer la variation d’entropie de l’eau.
Réponse
On prends un chemin réversible pour appliquer : $\Delta S = S_e$ $= m_g c_g ln(\frac{0°C}{T_g})$ $+ \frac{m_g \Delta _{fus}h}{0°C} + m_g c_e ln(\frac{T_f}{0°C})$
Application Numérique : $\Delta S = 10^{-3}. 2,10.10^3 ln(\frac{273}{273-18}) + \frac{333}{273}$ $+10^{-3} . 4,15.10^3 ln(\frac{273+20}{273})$ $=1,66 J.K^{-1}$
application numérique : $\Delta S = 24,9 J.K^{-1}$
Besoin d’aide pour cet exercice ? Cliquez ici !
EXERCICE 2
On place dans un verre, 20cL de soda à 18°C, on y ajoute un glaçon de 10g à -15°C. On néglige les échanges thermiques avec l’extérieur.
Question 1 : Enthalpie
1) Déterminer la température finale du milieu.
Déterminer la variation d’enthalpie permettra de remonter à la température finale du milieu.
Il y a 4 changements : la glace qui monte en température, la glace qui change d’état, le soda qui descend en température mais aussi l’eau liquide issue de la glace qui monte en température.
Réponse
$\Delta H = \Delta H_{soda} + \Delta H_{glace} + \Delta H_{glace->eau}$ $+ \Delta H_{eau-liquide}$ $= m_s c_s (T_f – T_i) + m_g c_g (0°C – T_g)$ $+ m_g \Delta _{fus} h$ $+m_g c_e(T_f – 0°c) =0$ car on a un échange interne, on isole $T_f$
On en déduit : $T_f = 283,2K = 10,2°C$
Question 2 : Entropie
2) Déterminer l’entropie créée.
Données : Enthalpie de fusion de l’eau à 0°C : $\Delta_{fus} H = 333J.g^{-1}$ ; Capacités thermiques massique de l’eau :$c_e=4,15 kJ.K^{-1}.kg^{-1}$, du soda : $c_s=2,60kJ.K^{-1}.kg^{-1}$ et de la glace : $c_g=2,10 kJ.K^{-1}.kg^{-1}$ .
Réponse
On prends un chemin réversible pour appliquer : $\Delta S = S_e$ $= m_s c_s ln(\frac{T_f}{T_i}) + m_g c_g ln(\frac{0°C}{T_g})$ $+ \frac{m_g \Delta _{fus}h}{0°C} + m_g c_e ln(\frac{T_f}{0°C})$
application numérique : $\Delta S = 0,78 J.K^{-1}$
Besoin d’aide pour cet exercice ? Cliquez ici !
Extrait du sujet 2024 A BCPST (voir le sujet corrigé complet)
B. DÉTENTE ET CROISSANCE DES BULLES DE CHAMPAGNE
Détente des bulles de champagne lors de l’ouverture de la bouteille
A l’ouverture d’une bouteille de champagne, un panache blanc qui fait penser à des microgouttelettes, se forme. Nous allons proposer une interprétation à ce phénomène. Le gaz présent dans la bouteille est composé principalement de dioxyde de carbone mais contient aussi de l’eau. Il est initialement sous une pression d’environ $𝑃_i = 6,0 bar$ et au moment de l’éjection du bouchon, il subit une détente adiabatique jusqu’à la pression atmosphérique $𝑃_f = 1,0 𝑏ar$ environ.
Pour interpréter simplement le panache, on se place dans le modèle d’une détente adiabatique réversible. Le gaz est supposé parfait, les capacités thermiques du gaz sont supposées indépendantes de la température. On donne l’expression de la variation d’entropie de 𝑛 mol d’un gaz parfait lors d’une transformation le conduisant d’un état initial $(𝑃_i, 𝑇_i)$ à un état final $(𝑃_f, 𝑇_f)$:
$\Delta S = C_P ln(\frac{T_f}{T_i}) – n R ln (\frac{P_f}{P_i})$
où $𝐶_p$ est la capacité thermique à pression constante du gaz.
13. Énoncer le second principe de la thermodynamique. Que vaut la variation d’entropie du gaz lors d’une détente adiabatique réversible ?
Second principe de la thermodynamique :
$\Delta S = S_c + S_e = S_c + \frac{\delta Q}{T}$
Avec $S_e$ : représente l’entropie échangée avec l’extérieur et $S_c$ l’entropie créée au sein du système.
$S_c >0$ pour les transformations irréversibles et $S_c=0$ pour les transformations réversibles.
-Dans le cas d’une détente adiabatique ($S_e=0$) réversible ($S_c=0$), alors $\Delta S = 0$, aussi appelé isentropique
14. Calculer la température $𝑇_f$ du gaz à l’issue de la détente. On donne pour le gaz dans la bouteille : température initiale $𝑇_i = 293 𝐾$ ; capacité thermique molaire à pression constante : $𝐶_P = 37 J. K^{−1}. mol^{−1}$ ; constante des gaz parfaits : $𝑅 = 8,31 J. K^{−1}. mol^{−1}$.
Nous sommes dans le modèle de la détente adiabatique réversible, donc $\Delta S = 0$
$\Rightarrow$ $ C_P ln(\frac{T_f}{T_i}) – n R ln (\frac{P_f}{P_i})=0$ $\Rightarrow$ $C_P ln(\frac{T_f}{T_i}) = n R ln (\frac{P_f}{P_i})$ $\Rightarrow$ $ ln((\frac{T_f}{T_i})^{C_P}) = ln ((\frac{P_f}{P_i})^{nR})$ $\Rightarrow$ $ (\frac{T_f}{T_i})^{C_P} = (\frac{P_f}{P_i})^{nR}$ $\Rightarrow$ $ T_f = T_i \times (\frac{P_f}{P_i})^{\frac{nR}{C_P}}$
Application Numérique :
$ T_f = 293 \times (\frac{1}{6})^{\frac{8,31}{37}} = 196,9K$ soit $-77,1°C$
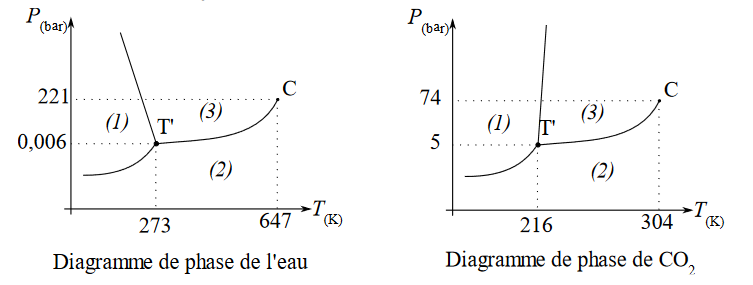
15. On donne ci-dessous les diagrammes de phase de l’eau et du dioxyde de carbone $CO_2$. Préciser les états du système dans les domaines 1, 2 et 3.
L’astuce est d’utiliser le diagramme de l’eau et de se placer à une pression de 1bar. Dans ce cas on sait que lorsque la température augmente, on passe de l’état solide à liquide puis gazeux.
Donc domaine 1 : état solide
domaine 3 : état liquide
domaine 2 : état gazeux
16. En s’appuyant sur les diagrammes précédents, proposer une explication à la formation de panache.
D’après les 2 diagrammes, en passant de l’état initial $P_i=6bar ; T_i = 293K$ à l’état final $P_i=1bar ; T_i = 196K$ l’eau et le $CO_2$ passent de l’état liquide à l’état solide créant un panache composé de glace d’eau et de $CO_2$ en suspension.
17. Pourquoi le modèle proposé n’est-il pas satisfaisant ?
Le modèle n’est pas satisfaisant car le $CO_2$ n’est pas un gaz parfait, On suppose également les capacités thermiques indépendants de la température ce qui n’est pas le cas ici car les variations de températures sont très importantes.