Physique BCPST2
Mécanique | Loi de Newton
C. FREINAGE D'UN TRAINEAU SUR LA GLACE
On s’intéresse ici au freinage sur la glace d’un traineau portant l’équipement et les instruments de mesure de l’expédition, la masse totale vaut 𝑚 = 80 𝑘𝑔 : à 𝑡 = 0, le traineau se trouve en O, origine du repère et se déplace horizontalement suivant l’axe x, l’axe z désignant l’axe vertical. Sa vitesse initiale vaut $𝑣_0 = 20 km.h^{−1}$ et il se déplace dans le sens de 𝑥 croissant. Il est alors soumis à une réaction $\vec{R}$ de la part de la glace et à une force de frottement $\vec{F}=-m \alpha v^2 \vec{u_x}$ de la part de l’air, où 𝑣 est la norme du vecteur vitesse et $\alpha$ une constante positive. On suppose que les lois de Coulomb du frottement solide s’appliquent de telle sorte que $𝑅_𝑇 = 𝑓𝑅_𝑁$ avec 𝑓, coefficient de frottement solide, $𝑅_𝑇$ et $𝑅_𝑁$ étant respectivement les valeurs absolues des composantes tangentielles et normales de la réaction $\vec{R}$. On cherche à déterminer le temps $𝑡_a$ mis par le traineau pour s’arrêter. On donne 𝑚 = 80 kg ; 𝑓 = 0,20 ; $𝑔 = 9,8 m.s^{-2}$ et $\alpha = 0,1 SI$.
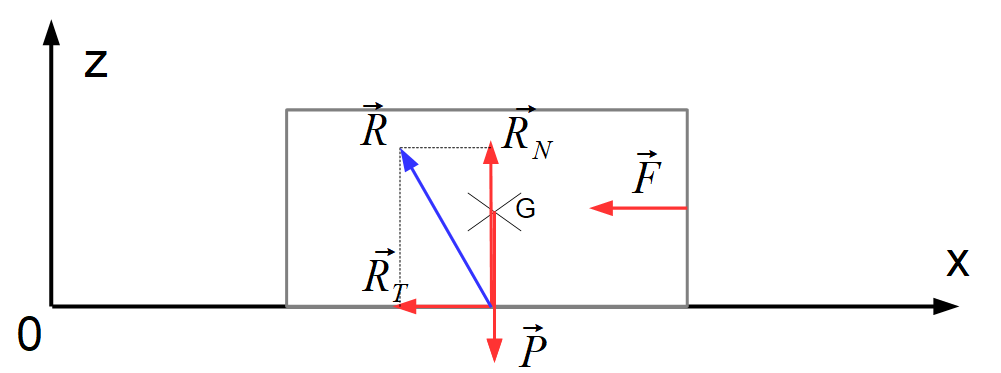
17. Faire un bilan des forces s’exerçant sur le skieur et les représenter sur un schéma.
Bilan des forces :
Le poids : $\vec P$ ; La force de frottement de l’air $\vec F$ ; La force de réaction $\vec R$ décomposée en force de réaction normale $\vec R_N$ et la force de réaction tangentielle $\vec R_T$ soit $\vec R = \vec R_N + \vec R_T$
18. Exprimer $𝑅_𝑁$ et $𝑅_𝑇$ en fonction de 𝑚, 𝑔 et 𝑓. Faire les applications numériques.
On applique la deuxième loi de Newton :
$\sum \vec F = m \vec a$
Si on projète sur l’axe (Oy) on obtient :
$R_N – P = m a_y =0$ ( $a_y=0$ car il n’y a pas de déplacements selon y)
$\rightarrow R_N=P=mg $
Application Numérique :
$ R_N= 80 \times 9,8 = 784N $
Il vient : $R_T = f R_N = fmg$
Application Numérique :
$R_T = 0,2 \times 80 \times 9,8 = 156,8N$
19. Exprimer 𝑅, la norme de $\vec R$ puis calculer sa valeur numérique.
$R = \sqrt{R_N^2 + R_T^2}$
Application Numérique :
$R = \sqrt{784^2 + 156,8^2} =800N$
20. Montrer que l’équation différentielle du mouvement peut se mettre sous la forme : $\frac{dv}{dt} = - \beta - \alpha v^2$. On exprimera $\beta$ en fonction de 𝑔 et 𝑓.
On projète le PFD sur l’axe (Ox) :
$-F – R_T = m a_x$
$-m \alpha v^2 – fmg = m a_x$
$a_x = \frac{dv}{dt} = -fg -\alpha v^2$
Par identification : $\beta = fg$
On donne ci-dessous un programme Python utilisant l’outil odeint du module scipy.integrate et permettant de résoudre numériquement l’équation différentielle précédente.
1 from scipy.integrate import odeint
2 import numpy as np
3 import matplotlib.pyplot as plt
4 g=9.8
5 alpha=0.10
6 f=0.2
7 beta= # à compléter
8 # Définition de l’équation différentielle
9 def derivee(v, t):
10 return -beta-alpha*v*v
11 t0 = 0
12 tf = 3 # seconde
13 v0 = # à compléter
14 t = np.linspace(t0, tf, 1000)
15 # Résolution
16 v = # à compléter
17 # tracés
18 plt.plot(t, v[:, 0], ‘b—’)
19 plt.ylabel(‘vitesse (m/s)’)
20 plt.xlabel(« Temps (s) »)
21 plt.grid()
22 plt.legend()
23 plt.show()
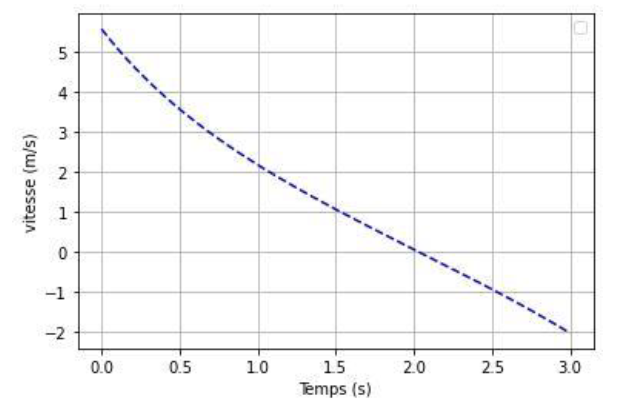
On obtient le graphe ci-dessous, représentant l’évolution temporelle de la vitesse :
21. Recopier et compléter les lignes 7, 13 et 16 du programme.
7. beta = f * g
13. v0 = 20/3,6
(attention au passage $km.h^{-1}$ en $m.s^{-1}$)
16. v = odeint(derivee,v0,t)
22. A partir du graphe ci-dessus, déterminer numériquement le temps d’arrêt $𝑡_a$ du mobile.
La vitesse devient nulle pour t=2s.

