Physique BCPST2
Transport Thermique | Flux thermique
E. BILAN THERMIQUE D'UN GLACIER
Les glaciers, de par leur faible inertie de réponse aux changements climatiques, sont des outils de choix pour comprendre l’augmentation globale de température observée depuis le XIXème siècle. La relation entre l’évolution des glaciers et la variabilité climatique repose en partie sur une étude du bilan d’énergie de surface du glacier. Pour effectuer ce bilan, on considère le volume compris entre la surface et une profondeur à partir de laquelle il n’existe plus de flux radiatifs significatifs comme l’indique la figure ci-dessous.
Nous allons effectuer un bilan en termes de flux surfacique pour déterminer l’énergie stockée par unité de surface et par unité de temps, du volume étudié, que l’on notera Φ ; cette dernière a pour effet d’augmenter ou de diminuer la température de la glace et peut également induire la fonte de la glace ou la solidification de l’eau liquide.
Le bilan fait apparaître les flux suivants (chaque flux est positif s’il est reçu par la surface, et négatif s’il est cédé par la surface) :
• Des flux surfaciques radiatifs arrivant « in » et partant « out » de la surface notés $𝑆𝑊_{in}$ et $𝑆𝑊_{out}$ pour les radiations de courtes longueurs d’onde (Short Waves de longueur d’onde comprise entre 0,15 et 3 μ𝑚) et $𝐿𝑊_{in}$ et $𝐿𝑊_{out}$ (Long Waves) pour les radiations de grandes longueurs d’onde (de 3 à 100 μ𝑚) ;
• Des flux surfaciques de convection : 𝐿𝐸 le flux turbulent de chaleur latente (permet à la neige de se sublimer une fois au sol ; il dépend de la vitesse du vent, de l’humidité mais aussi de la densité de l’air et de la chaleur latente de sublimation) et 𝐻 le flux turbulent sensible (permet à la neige déposée de changer de température ; il dépend de la densité de l’air, de la capacité thermique massique à pression constante de l’air mais aussi de la vitesse du vent et de la température de la neige) ;
• Du flux surfacique 𝑃 induit par les précipitations ;
• Du flux surfacique conductif 𝐺 dans la neige/glace.
On ne s’intéresse qu’à des flux verticaux par rapport au volume de glace étudié, supposé horizontal et on se place en géométrie axiale d’axe 𝑂𝑧. Aucune connaissance spécifique sur le transfert thermique par rayonnement n’est nécessaire pour traiter cette partie.
Un corps noir de température absolue 𝑇 émet un rayonnement thermique. La loi de Wien donne la longueur d’onde pour laquelle l’émittance (puissance émise par unité de surface du corps noir et par unité de longueur d’onde) est maximale à la température 𝑇 du corps noir :
$𝜆_{max} = \frac{𝑐𝑡𝑒}{𝑇}$ avec $𝑐𝑡𝑒 = 2,898. 10^{−3} m.K$.
La loi de Stefan-Boltzmann donne l’expression de la puissance surfacique rayonnée (émittance énergétique totale, prenant en compte toutes les longueurs d’onde) :
$𝜙_{𝑡ℎ}(𝑇) = 𝜎𝑇^4$
$𝜎 = 5,67. 10^{−8} W.m^{-2}.K^{-4}$ est la constante de Stefan-Boltzmann.
33. Qu’est-ce-qui distingue les transferts thermiques par conduction ou convection des transferts thermiques par rayonnement ? Qu’est-ce-qui distingue les transferts thermiques par conduction des transferts thermiques par convection ?
-Les transferts thermiques par conduction ou convection ont besoin d’un support pour se propager contrairement au rayonnement qui peut se propager dans le vide.
-Dans les transferts thermiques par conduction, il n’y a pas de déplacement de la matière, le déplacement se fait de proche en proche.
34. Justifier, par un calcul de longueur d’onde en μ𝑚, que les radiations courtes longueurs d’onde sont dues au Soleil (température moyenne $𝑇_S = 5778 K$) alors que les radiations grandes longueurs d’onde sont dues au système terrestre (température moyenne $𝑇_T = 300 K$).
On calcul $\lambda_{max}$ pour le Soleil et la Terre :
$\lambda_{max,Soleil} = \frac{cte}{T}$ $=\frac{2,898.10^{-3}}{5778}$ $=0,5µm$ (ordre de grandeur des courtes longueurs d’ondes)
$\lambda_{max,Terre} = \frac{cte}{T}$ $=\frac{2,898.10^{-3}}{300}$ $=9,7µm$ (ordre de grandeur des grandes longueurs d’ondes)
35. Calculer le flux radiatif $𝐿𝑊_{out}$ dans le cas où la neige/glace se comporte comme un corps noir de température égale à −2,6°C.
$LW_{out} = \sigma T^4$ , le signe sera négatif car l’énergie est cédé par la surface.
Application Numérique :
$LW_{out} = -5,67.10^{-8} . (273-2.6)^4$ $= -303 W.m^{-1}$
36. On note 𝑅 le flux radiatif global. Exprimer 𝑅 en fonction de $𝑆𝑊_{in}, 𝑆𝑊_{out}, 𝐿𝑊_{in} et 𝐿𝑊_{out}$.
$R = SW_{in} + SW_{out} + LW_{in} + LW_{out}$
R représente la somme des flux. La valeur de chaque flux aura un signe positif ou négatif en fonction de l’énergie cédée ou reçue.
37. Le flux diffusif 𝐺 suit la loi de Fourier. Donner l’expression de 𝐺 dans ce contexte en précisant les unités et la signification physique des différents termes.
$G = \frac{P_{th}}{S} = – \lambda \frac{dT}{dz}$
Avec G: Le flux surfacique (en $W.m^{-2}$). Représente le flux de chaleur qui passe à travers une surface de contrôle.
$\lambda$ : conductivité thermique (en $W.m^{-1}.K^{-1}$). Grandeur intrinsèque au matériau qui caractérise la capacité de diffuser la chaleur.
$d T$ : Variation de température (en Kelvin : K). Représente la variation de température entre 2 surfaces de contrôles. La variation de la température est la cause qui permet le déplacement du flux de chaleur.
dz : Longueur caractéristique (en mètre : m) entre les 2 surfaces de contrôles.
38. Que vaut 𝐺 dans le cas d’un glacier isotherme ?
Si le glacier est isotherme, on a dT =0 soit un flux surfacique G = 0.
39. Le flux surfacique apporté par les précipitations suit une loi de type loi de Newton : donner l’expression de 𝑃 en fonction du coefficient de transfert thermique ℎ, de la température de la neige qui tombe $𝑇_n$ et de la température de la surface du glacier $𝑇_{surf}$ dans le cas$ 𝑇_n > 𝑇_{surf}$.
On a $T_n > T_{surf}$, ce qui implique un flux de chaleur de la neige vers le glacier (le flux de chaleur se dirige toujours de la température la plus élevé vers la température la moins élevée). Le glacier reçoit donc de la chaleur, le flux surfacique P doit être positif.
$P = \frac{\Phi}{S} = h \Delta T$ $=h (T_n – T_{surf})$
Le coefficient ℎ dépend de la masse volumique de la neige 𝜌, de sa capacité thermique massique $𝑐_n$ et de l’intensité 𝐼 de précipitation : $ℎ = 𝜌^a 𝑐_n^b 𝐼^c$.
Par la suite, on prendra $𝜌 = 0,20 kg.L^{−1}$, $𝑐_n =2090 J.K^{−1}.kg^{−1}$ et $𝐼 =2,0 mm.heure^{−1}$.
40. Par analyse dimensionnelle, déterminer a, b et c et exprimer ℎ en fonction de 𝜌, $𝑐_n$ et 𝐼
L’unité de h est en $W.m^{-2}.K^{-1}$
Si on analyse $[\rho] \times [c_n] \times [I]$, on retrouve : $\frac{M}{L^3} \times \frac{J}{K . M} \times \frac{L}{T}$ $=\frac{J}{L^2 . K . T}$ soit $J.m^{-2}.K^{-1}.s^{-1}$, or le $J.s^{-1}=W$ ce qui donne une unité en $W.m^{-2}.K^{-1}$ ce qui correspond à l’unité de h.
On retrouve alors $a=b=c=1$ soit : $h= \rho c_n I$
41. Faire l’application numérique sur 𝑃 lorsque la différence de température entre la neige qui tombe et la surface du glacier vaut 5 °𝐶.
$P=h \Delta T$ $=\rho . c_n.I. \Delta T$
(attention aux unités!)
Application Numérique :
$P= 0,20.10^3 \times 2090 \times (\frac{2.10^{-3}}{3600}) \times (273+5)$ $=64,6W.m^{-2}$
42. Compléter sur l'annexe, le schéma en indiquant les flux énergétiques et en précisant leur sens par une simple flèche (voire une double flèche si le sens du flux n’est a priori pas connu).
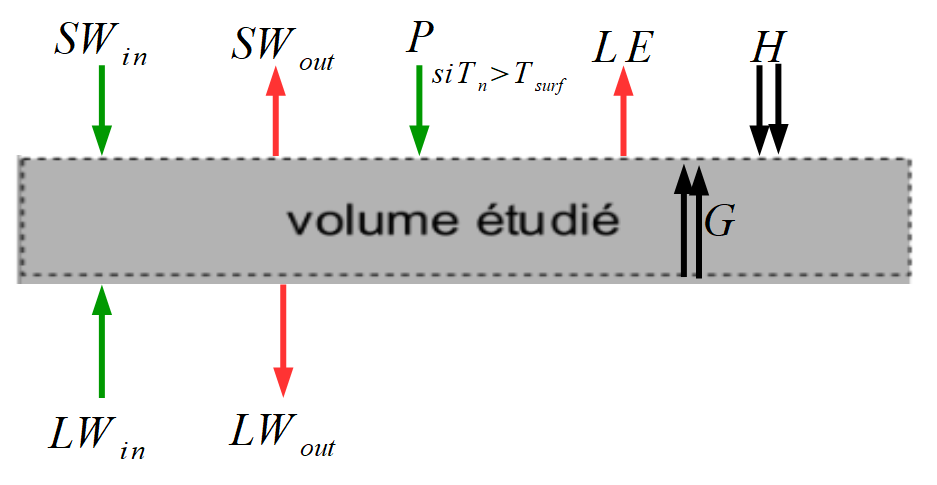
Les flux radiatifs SW et LW sont positifs si ils sont entrants et négatifs si ils sont sortants.
Le flux P est positif si $T_n>T_{surf}$, (ce qui est le cas ici) négatif sinon.
Le flux LE permet à la neige de se sublimer et a donc besoin de l’énergie de la surface, donc c’est un flux sortant.
Le flux H dépend de la température de la neige et de la surface ainsi que d’autres paramètres non accessible donc le sens n’est pas défini.
Le flux G dépend des températures de la surface supérieure et inférieure. Paramètres non donnés donc le sens ne peut être défini.
43. A l’aide d’un bilan thermique, exprimer l’énergie stockée Φ par unité de surface et unité de temps en fonction des flux surfaciques 𝑅, 𝐿𝐸, 𝐺, 𝐻 et 𝑃.
$\Phi = R + LE + G + H+ P$
44. Calculer Φ lorsque $𝑅 =15,8 W.m^{−2}$, $𝐿𝐸 = −18,1 W.m^{−2}$ et $𝐻 = 6,1 W.m^{−2}$.
Application Numérique :
$\Phi = 15,8 – 18,1 + 0 +6,1+ 64,6$ $=68,4W.m^{-2}$
45. En raisonnant sur le signe de l’énergie stockée, expliquer en respectant l’ordre chronologique les phénomènes ayant lieu dans la neige/glace.
On retrouve une énergie positive donc une énergie reçu par le glacier qui aura comme conséquence une élévation de sa température.
Par ordre chronologique (ceci est une suggestion de réponse) :
On a tout d’abord le flux $SW_{in}$ du Soleil puis par réflexion $SW_{out}$. Vient également les flux $LW_{in} et LW_{out}$ issus de la Terre.
Dans l’atmosphère ces flux peuvent créer des précipitations (flux P) qui une fois au sol créées un flux H et/ou LE.
Enfin le flux G existera si il y a une différence de température sur la face supérieure et inférieure de la glace.


