Physique BCPST1
Mécanique | Équation horaire
SLALOM A SKI DANS UNE FORET
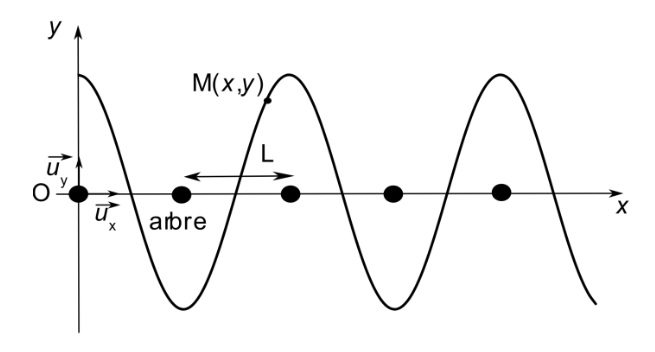
Afin de rejoindre le glacier, l’équipe scientifique traverse à ski une forêt. Un skieur, assimilé à un point matériel M, réalise un slalom dans une forêt où les arbres sont supposés régulièrement espacés d’une distance 𝐿 = 100 m suivant l’axe 𝑂𝑥 de la pente (voir figure ci-dessous). On note 𝑂𝑦 la direction horizontale perpendiculaire à la pente (𝑂𝑥). A 𝑡 = 0, le skieur se trouve en $M_0$ (0, $y_0$). On suppose que le skieur suit une trajectoire sinusoïdale $𝑦(𝑥) = 𝑦_0 . cos(𝑘𝑥)$ et qu’il conserve à tout moment une vitesse dont la composante suivant 𝑂𝑥 est constante : $𝑥̇ = 𝑣_0 = 30 km.h^{−1}$. On s’intéresse ici à l’étude cinématique du mouvement du skieur, décrivant une trajectoire sinusoïdale :
12.Exprimer 𝑘 en fonction de 𝐿.
Pour la position en y(t), on retrouve la périodicité du cosinus tous les 2 $\pi$ lorsque l’on atteint une distance de 2L , $cos(kx) = cos(kx +2 \pi )$
Ici, $cos(0) =cos(2 \pi) = cos(k 2L )$,
soit : $k2L=2\pi $ ce qui nous donne $k = \frac{\pi}{L}$
$y(x)=y_0 cos(\frac{\pi x}{L})$
13.Exprimer 𝑥(𝑡) puis 𝑦(𝑡)
$x(t) = v_0 t + x_0$ $= v_0 t$
on remplace x dans y(x)
$y(t) = y_0 cos(\frac{\pi v_0 t}{L})$
14.En déduire l’expression de la période temporelle 𝑇 des oscillations du skieur en fonction de 𝐿 et de $𝑣_0$. Faire l’application numérique sur 𝑇.
On peut réecrire $y(t) = y_0 cos(\omega t )$ avec $\omega$ la pulsation, ici $\omega = \frac{2 \pi}{T}$.
$\frac{2 \pi}{T} = \frac{\pi v_0}{L}$ \rightarrow$ $T=\frac{2L}{v_0}$
Application Numérique :
$T = \frac{2 \times 100}{\frac{30}{3.6}}$ $=24s$
15. Donner les expressions des vecteurs vitesse $\vec{v}$ et accélération $\vec{a}$ du skieur sur la base cartésienne ($\vec{u_x}, \vec{u_y}$).
Vecteur vitesse :
$\vec{v} = v_0 \vec{u_x} + \dot{y}(t) \vec{u_y}$ $=v_0 \vec{u_x} – y_0 \frac{\pi v_0}{L}sin(\frac{\pi v_0 t}{L}) \vec{u_y}$
Vecteur accélération :
$\vec{a} = 0 . \vec{u_x} – y_0 (\frac{\pi v_0}{L})^2 cos(\frac{\pi v_0 t}{L}) \vec{u_y}$
16. Pour que le skieur reste debout, il doit avoir une accélération inférieure à $0,7𝑔$ où $𝑔 = 9,8 m.s^{−2}$ est l’accélération de la pesanteur. Quelle est alors l’amplitude maximale $𝑦_{0,max}$ que peut adopter le skieur sans chuter ? Faire l’application numérique sur $𝑦_{0,max}$.
On a l’accélération maximale pour $cos(\frac{\pi v_0 t}{L})=1$ $\rightarrow$ $-y_0 (\frac{\pi v_0}{L})^2 \lt a_{max}= 0.7g$
$y_{0,max} = \frac{0.7 g L^2}{(\pi v_0)^2}$
Application Numérique :
$y_{0,max} = \frac{0.7 \yimes 9,8 \times 100^2}{(\pi \frac{30}{3,6})^2}$ $=100m$