Physique BCPST2
Mécanique des fluides | Contrainte tangentielle
D. ÉCOULEMENT D'UN GLACIER
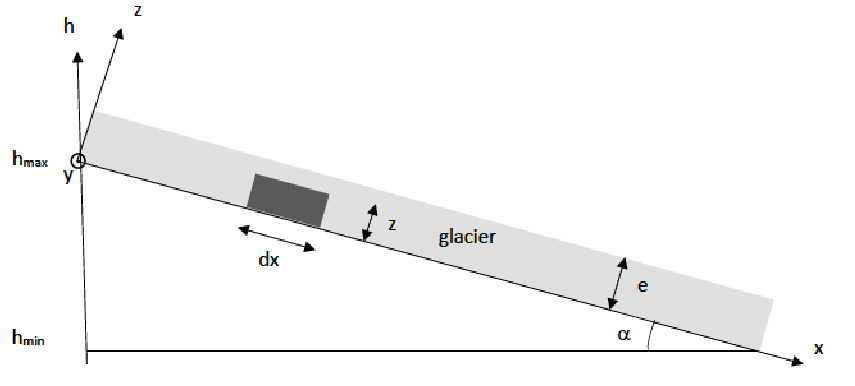
On s’intéresse à l’écoulement du glacier des Bossons dans la vallée de Chamonix : l’altitude maximale du glacier est $ℎ_{max} = 4700 m$ et son altitude minimale $ℎ_{min} =1400 m$. La pente moyenne du glacier, supposée constante, fait un angle $\alpha = 28° $ avec l’horizontale ; son épaisseur supposée constante est 𝑒 = 120 m et sa largeur supposée constante est 𝐿 = 1200 m (suivant la direction (𝑂𝑦) perpendiculaire au schéma). On adopte le système d’axes représenté ci-dessous : (𝑂𝑥) est dirigé suivant la pente du glacier et (𝑂𝑧) dirigé suivant la hauteur du glacier. On donne : la masse volumique de la glace $\rho_{glace} = 920 kg.m^{−3}$ ; la viscosité dynamique de la glace considérée comme un fluide newtonien $\eta_{glace} =1,0.10^{10} Pa.s $; l’accélération de la pesanteur $𝑔 = 9,8 m.s^{−2}$.
En 1966 a eu lieu le crash d’un Boeing 707 d’Air India au sommet du glacier. Parmi la cargaison, des pierres précieuses ont été retrouvées au bas du glacier en 2013 par un randonneur chanceux.
Régime d’écoulement du glacier
23. Exprimer littéralement puis calculer numériquement en tonnes, la masse $𝑚_{glace}$ du glacier.
La masse du glacier $m =\rho \times V$ avec V : volume du glacier = $e\times L \times l$, ici $l$ représente la longueur de la pente (soit l’hypoténuse du triangle).
On retrouve $sin \alpha = \frac{(h_{max} – h_{min})}{l}$ , soit $l=\frac{(h_{max} – h_{min})}{sin \alpha} $
On retrouve une masse $m= \frac{\rho \times e \times L \times (h_{max}- h_{min})}{sin \alpha}$
Application Numérique :
$m= \frac{920 \times 120 \times 120 \times (4700- 1400)}{sin 28}$ $=9,3.10^{11} kg$ $=9,3.10^8 tonnes$
24. A l’aide des données, exprimer littéralement puis calculer numériquement la vitesse d’écoulement 𝑈 du glacier.
On peut utiliser l’information donnée après le schéma. Les pierres précieuses ont parcourues la distance $l$ en 47ans. Elles avancent à la même vitesse que le glacier.
Soit $U = \frac{d}{\Delta t}$ $=\frac{h_{max}-h_{min}}{sin \alpha \times \Delta t}$
Application Numérique :
$U =\frac{4700 -1400}{sin 28 \times 47}$ $=149,6 m.an^{-1}$ $=4,74.10^{-6} m.s^{-1}$
25. Définir puis calculer le nombre de Reynolds 𝑅e associé à l’écoulement du glacier. Conclure sur la nature de l’écoulement.
Nombre de Reynolds : $R_e = \frac{U \times L}{\nu}$ $=\frac{\rho \times U \times L}{\eta}$
Application Numérique :
$R_e =\frac{920 \times 4,74.10^{-6} \times 1200}{1,0.10^{10} }$ $=5,25.10^{-10}$
C’est un écoulement rampant.
Profil des vitesses dans une section droite du glacier
On s’intéresse à l’écoulement d’une particule fluide de hauteur 𝑧 et de surface d𝑆 = 𝐿d𝑥, et représentée sur la figure précédente.
On suppose que le glacier s’écoule sous l’effet de son poids en régime permanent, de telle sorte que la force de viscosité $d𝐹 = 𝜏_T d𝑆$ est compensée par la composante tangentielle du poids.
26. Exprimer la contrainte tangentielle visqueuse $𝜏_T(𝑧)$ en fonction de $\rho_{glace}$, 𝑔, 𝑧 et $\alpha$.
Sur le schéma on peut placer $\vec dF$ et le poids décomposé en sa composante tangentielle et sa composante normale.
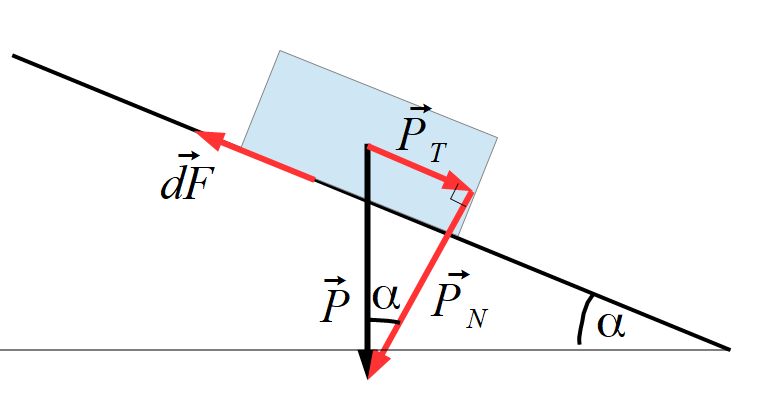
L’énoncé nous donne l’égalité entre la force de viscosité dF et la composante tangentielle du poids $P_T$
$dF=P_T $ $\rightarrow$ $ \tau _T dS = P sin \alpha = mg sin \alpha$ $=\rho_{glace} V g sin \alpha$ $=\rho_{glace} z dS g sin \alpha$ soit :
$\tau _T = \rho_{glace} z g sin \alpha$
27. En déduire l’expression de $𝜏_T(𝑒)$ puis faire l’application numérique. Comparer la valeur obtenue à la pression atmosphérique.
$\tau_T(e) = \rho_{glace} g e sin \alpha$
Application Numérique :
$\tau_T(e) = 920 \times 9,8 \times 120 \times sin (28)$ $=5,08.10^5 Pa$
On retrouve $\tau_T(e) \simeq 5 \times P_{atm}$
On suppose que la relation entre le gradient des vitesses (ou taux de cisaillement) $\dot \gamma = \frac{dU}{dz}$ et la contrainte tangentielle visqueuse $𝜏_T(𝑧)$ suit la loi de Glen : $\dot \gamma = \frac{dU}{dz} = 𝐴(𝑇) \tau_𝑇 ^3 $ avec 𝐴(𝑇) un facteur dépendant de la température 𝑇 selon la loi : $𝐴(𝑇) = 𝐴_0 e^{− \frac{Q}{RT}}$ où 𝑄 désigne l’énergie d’activation (en $J.mol^{−1}$) associée au phénomène et 𝑅 la constante des gaz parfaits. On se placera à une température égale à 𝜃 = −10 °𝐶 .
28. La glace peut-elle être considérée comme un fluide visqueux newtonien ? Justifier.
Un fluide Newtonien est un fluide dont la loi $contrainte-vitesse de déformation$ doit être linéaire, ce n’est pas le cas ici, le glacier est donc un fluide visqueux non Newtonien.
29. On qualifie la relation 𝐴(𝑇) d’arrhénienne. Justifier ce qualificatif et donner l’influence de la température sur l’écoulement.
A(T) est une relation arrhénienne car elle dépend de la température en $A e^{1/T}$ équivalent à la loi d’Arrhénius : $k=A e^{- \frac{E_a}{RT}}$.
Ici si T augmente alors A(T) augmente (évolution en $e^{-x}$ avec x décroissant) .
30. On cherche à déterminer le profil des vitesses 𝑈(𝑧). Justifier que 𝑈(0) = 0.
U(0) correspond à la vitesse de la couche directement en contact avec le sol. La couche de fluide visqueux directement en contact avec la paroi à la vitesse de la paroi. Ici le sol est immobile donc U(0)=0.
31. Intégrer, par séparation des variables, la loi de Glen pour en déduire le profil des vitesses 𝑈(𝑧).
Loi de Glen : $\frac{dU}{dz} = 𝐴(𝑇) \tau_𝑇 ^3 $
Séparation des variables :$dU = 𝐴(𝑇) (\rho_{glace} . z . g . sin\alpha)^3 dz$
Intégration :
$ \int_{U(0)}^{U(z)} dU = \int_{0}^{z} 𝐴(𝑇) (\rho_{glace} . g . sin\alpha)^3. z^3 . dz$ $\Rightarrow$ $U(z) – U(0) = A(T) (\rho_{glace} . g . sin \alpha)^3 [\frac{z^4}{4}]_0^z$
$U(z) = \frac{A(T) (\rho_{glace} .g.sin \alpha)^3 . z^4}{4} $
32. En déduire 𝑈(𝑒) et faire l’application numérique. On donne : $𝐴 = 10^{−24}$ pour 𝜃 = −10 °𝐶. Comparer au résultat de la question 24.
$U(e) = \frac{A(T) (\rho_{glace} .g.sin \alpha)^3 . e^4}{4} $
Application Numérique :
$U(e) = \frac{10^{-24} (920 \times 9,8 \times sin (28))^3 . 120^4}{4} $ $=3,9.10^{-6} m.s^{-1}$
Le résultat est proche de celui de la question 24 ($4,76.10^{-6}m.s^{-1}$)