Physique BCPST1
Optique | Loi Snell Descartes
EXERCICE 1 : Cas simple
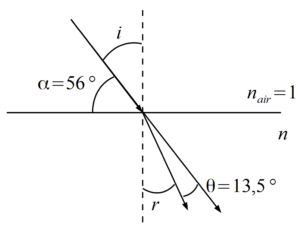
Un rayon lumineux dans l’air tombe sur la surface d’un liquide, il fait un angle $α=56°$ avec le plan horizontal. La déviation entre le rayon incident et le rayon réfracté est $θ = 13,5°$. Quel est l’indice $n$ du liquide ?
Réponse
Attention aux piège sur la valeur de l’angle $\alpha$ car cet angle ne correspond pas à l’angle d’incidence. L’angle d’incidence correspond à l’angle entre le rayon incident et la normale à la surface soit : $i=90 – 56=34°$
Le milieu 2 est plus réfringent donc le rayon se rapproche de la normale de $13,5°$, on en déduit que l’angle réfracté vaut $r=34-13,5=20,5°$.
On peut utiliser la loi de Snell-Descartes :
$n_{air} sin(i) = n sin(r)$ $\Rightarrow$ $n = \frac{sin(i)}{sin(r)}$
Application Numérique :
$n=\frac{sin(34)}{sin(20,5)}= 1,60$
EXERCICE 2 : (extrait G2E 2023) Jumelles à prismes
Extrait du sujet 2023 G2E voir le sujet corrigé complet
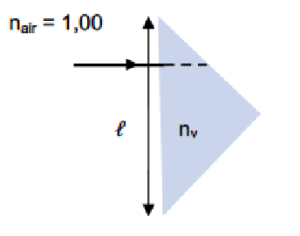
On utilise pour les observations une jumelle qui contient un objectif, un dispositif redresseur à base de prismes et un oculaire. On commence par étudier le trajet de la lumière à travers un prisme rectangle isocèle, en verre d’indice $𝑛_v$ = 1,50. Pour des raisons de clarté, le prisme est représenté en coupe dans le plan d’incidence. On s’intéresse à un rayon lumineux arrivant sur la normale du prisme comme indiqué sur la figure ci-dessous :
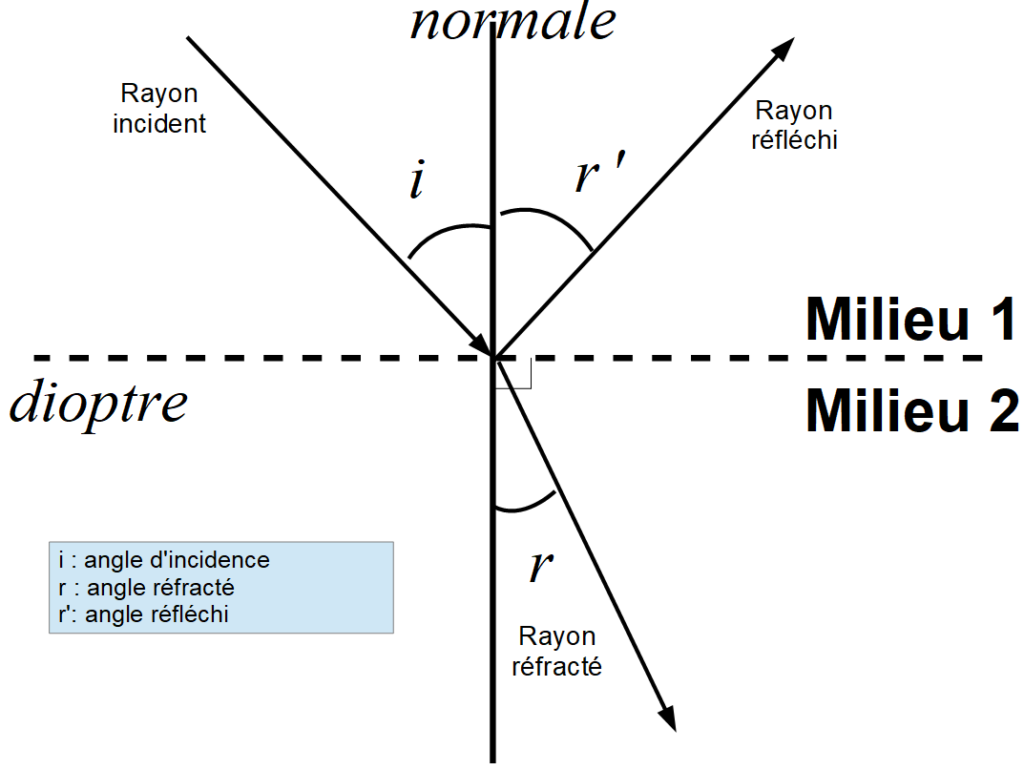
6. Rappeler les lois de la réflexion et les lois de la réfraction de Snell-Descartes en vous appuyant sur un schéma.
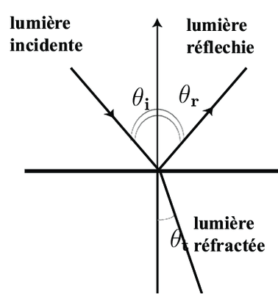Soit un rayon en incidence quelconque sur un dioptre séparant 2 milieux d’indice différents ($n_1$ et $n_2$). Ici nous ne donnons pas de sens aux angles.
Le rayon réfléchi, le rayon réfracté, le rayon incident et la normale (au dioptre) sont contenus dans le plan d’incidence.
Loi de la réflexion :
les angles incidents et réfléchis sont égaux $\theta_i = \theta_r$
Loi de la réfraction :
La relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incident θi et réfracté θt, appelée relation de Snell-Descartes, s’écrit :
$n_1 sin(\theta_i) = n_2 sin(\theta_t)$
7. L’indice de l’air extérieur dans lequel baigne le prisme est égal à 1,00. Calculer la valeur limite de l’indice du prisme noté $n_{V,lim}$ assurant la réflexion totale à l’interface verre-air
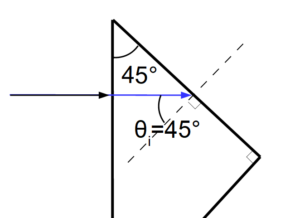
Le rayon dans le prisme atteint l’interface prisme/air avec un angle incident de 45°. Pour connaitre la valeur de l’indice minimale du prisme il faut considérer que l’angle réfracté a atteint la valeur de 90°. On obtient la relation :
$n_{V,lim} sin(\theta_i) = n_{air} sin(\theta_r)$, soit $n_{V,lim} = \frac{n_{air} sin(\theta_r)}{sin(\theta_i)}$
Application Numérique :
$n_{V,lim} = \frac{1 \times sin(90)}{sin(45)}$ $=1,41$
8. Représenter sur votre copie le trajet d’un rayon lumineux qui, une fois entré dans le prisme, est réfléchi sur les deux faces du prisme. Préciser la direction du rayon sortant du prisme.
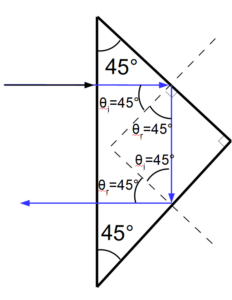
Les angles incidents et réfléchis sont tous égaux à 45° par conséquent le rayon revient parallèle au rayon incident.
9. Par des considérations géométriques, montrer que la distance parcourue dans le prisme par le rayon lumineux vaut ℓ, longueur de l’hypoténuse.
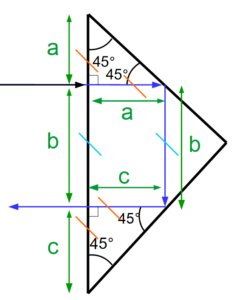
Ici $a+b+c = l$ (hypothénuse) or en haut et en bas on retrouve 2 triangles rectangles isocèles donc les chemins horizontaux du rayon correspond aux cotés a et c. (Ils sont d’ailleurs égaux entre eux : a = c)
Enfin les rayons dans le prisme ainsi que le coté b du prisme forment un rectangle, donc les cotés b sont égaux.
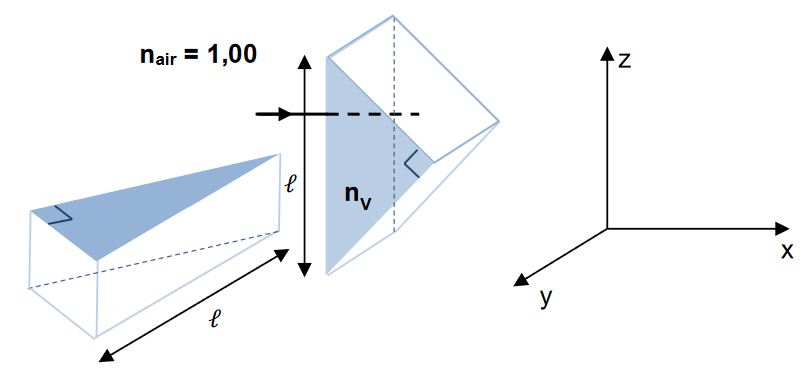
On s’intéresse maintenant au dispositif redresseur complet mettant en œuvre 2 prismes isocèles rectangles dont les hypoténuses sont perpendiculaires entre elles et à la direction initiale du faisceau incident. Le faisceau incident se propage suivant l’axe 𝑥. L’hypoténuse du premier prisme est orientée suivant 𝑧 et celle du second prisme suivant 𝑦.
10. Représenter sur l'annexe à joindre avec la copie, le trajet d’un rayon lumineux qui rentre dans le redresseur. Préciser la direction du rayon sortant du dispositif.
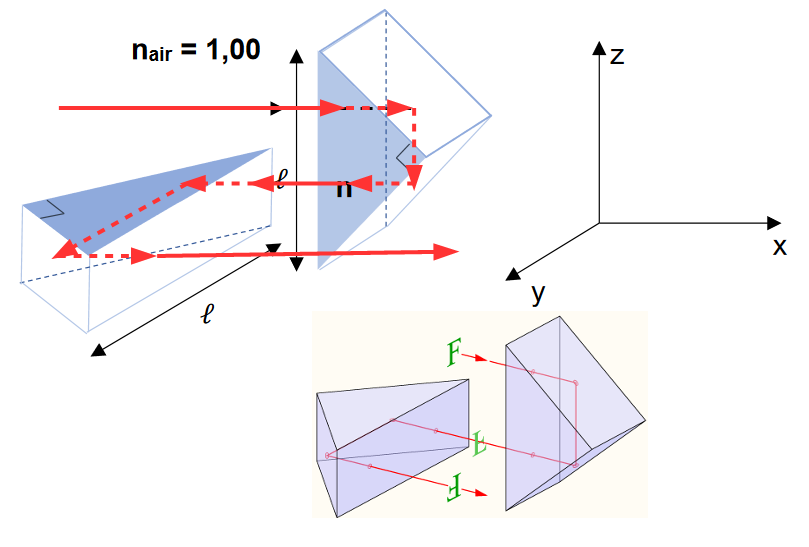
Le rayon sortant est parallèle au rayon entrant.
11. Outre son caractère redresseur, le dispositif précédent permet un gain de chemin optique, ce dernier étant défini comme le produit de l’indice du milieu par la distance parcourue. Evaluer le gain en chemin optique noté $\Delta$ apporté par le dispositif à prismes en supposant les prismes accolés.
A la question 9 nous avons démontré que le chemin du rayon dans le prisme est égal à $l$ (hypoténuse du prisme). Dans le redresseur, le rayon traverse 2 prismes identiques, le rayon parcours alors une distance 2$l$.
Le gain, défini comme le produit de l’indice du milieu par la distance parcourue est égal à : $\Delta = n_v \times 2 \times l$
Physique BCPST
A BCPST | 2023
Extrait du sujet 2023 A BCPST voir le sujet corrigé complet
Données numériques utiles
Célérité de la lumière dans le vide $𝑐 = 3,0 × 10^8 m.s^{−1}$
Indice optique de l’air $𝑛_𝑎 = 1,00$
Indice optique de la glace $𝑛_𝑔 = 1,31$
Masse volumique de la glace $𝜌_𝑔 = 0,917 × 10^3 kg.m^{−3}$
Masse volumique de l’eau liquide $𝜌_ℓ = 1,0 × 10^3 kg.m^{−3}$
Enthalpie massique de fusion de la glace $ℓ_𝑓 = 333,5 kJ.kg^{−1}$
Capacité thermique massique de l’eau liquide $𝑐_ℓ = 4,18 kJ.kg^{−1}.K^{−1}$
Rayon de la Terre $𝑅_𝑇 = 6 400 km$
Norme de l’accélération de la pesanteur $𝑔 = 9,8 m.s^{−2}$
EXERCICE 3 : (extrait A BCPST 2023) Modélisation du halo solaire
I. La réfraction de la lumière
1. On considère un milieu homogène, isotrope et transparent à la lumière. Exprimer l’indice optique 𝑛 de ce milieu en fonction de la célérité 𝑣 de la lumière dans ce milieu et de la célérité 𝑐 de la lumière dans le vide.
L’indice optique représente la rapport entre la vitesse de la lumière dans le vide et celle dans le milieu, soit :
$n=\frac{c}{\nu}$
L’indice optique est toujours supérieur à 1.
On étudie la situation, représentée sur la figure 1 suivante, de la réfraction et de la réflexion de la lumière.
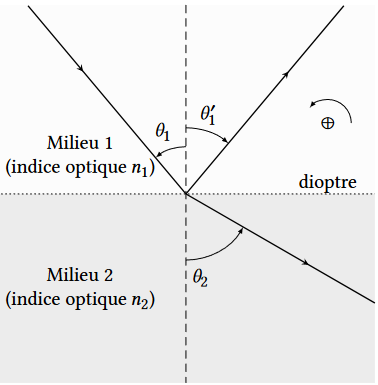
Un rayon lumineux incident arrive sur un dioptre qui sépare deux milieux d’indices optiques $𝑛_1$ et $𝑛_2$.
On note $𝜃_1$ l’angle d’incidence du rayon incident, $𝜃′_1$ l’angle que le rayon réfléchi fait avec la normale
au dioptre, et $𝜃_2$ l’angle que le rayon réfracté fait avec cette même normale. Les angles considérés sont algébriques ; le sens positif, qui correspond au sens trigonométrique, est défini sur la figure 1 avec le symbole ⊕.
Figure 1 – Réflexion et réfraction de la lumière par un dioptre ($𝑛_2 < 𝑛_1$). Les différents angles sont orientés : $𝜃_1 > 0$, $𝜃′_1 < 0$ et $𝜃_2 > 0$. Le sens positif est le sens trigonométrique.
2. Rappeler les lois de la réflexion et de la réfraction de Snell-Descartes.
Soit un rayon en incidence quelconque sur un dioptre séparant 2 milieux d’indice différents ($n_1$ et $n_2$). Ici nous ne donnons pas de sens aux angles.
Le rayon réfléchi, le rayon réfracté, le rayon incident et la normale (au dioptre) sont contenus dans le plan d’incidence.
Loi de la réflexion :
les angles incidents et réfléchis sont égaux $\theta_i = \theta_r$
Loi de la réfraction :
La relation liant les indices de réfraction n1 et n2 de chacun des milieux et les angles incident θi et réfracté θt, appelée relation de Snell-Descartes, s’écrit :
$n_1 sin(\theta_i) = n_2 sin(\theta_t)$
3. Montrer que, dans le cas où $𝑛_2 < 𝑛_1$, si $𝜃_1$ est supérieur à une valeur $𝜃_ℓ$, l’énergie véhiculée par le rayon incident est totalement réfléchie par le dioptre. Nommer cette situation.
Si $n_2<n_1$ $\Rightarrow$ $\frac{n_2}{n_1}<1$, or $\frac{n_2}{n_1}=\frac{sin(\theta_1)}{sin(\theta _2)}<1$ $\Rightarrow$ $\theta_1 < \theta_2$ car sinus est une fonction croissante sur l’intervalle $[0:\frac{\pi}{2}]$
Il y a donc une valeur limite de $\theta_1$ au delà de laquelle l’onde est totalement réfléchie, on parle d’angle limite et de réflexion totale.
4. Exprimer $𝜃_ℓ$ en fonction de $𝑛_1$ et $𝑛_2$.
On a $\theta_l$ lorsque $\theta_2 = \frac{\pi}{2}$.
$n_1 sin(\theta_l)= n_2$ $\Rightarrow$ $\theta_l = arcsin(\frac{n_2}{n_1})$
5. Dans le cas d’un dioptre séparant la glace (milieu 1) de l’air (milieu 2), calculer la valeur de $𝜃_ℓ$ en degrés.
$\theta_l = arcsin(\frac{n_a}{n_g})$
Application Numérique :
$\theta_l = arcsin(\frac{1,00}{1,31})$ $=49,8°$
II. Le halo solaire
Le halo solaire, ou anthélie, est un phénomène optique atmosphérique qui ressemble à un arc-en-ciel circulaire (voir figure 2 à gauche). Il apparaît sous la forme d’un cercle coloré dont le soleil occupe le centre. L’objectif de cette sous-partie est la détermination du rayon angulaire du halo (qui représente l’angle au sommet du cône représenté sur la figure 2 à droite).
Le halo est dû à la réfraction de la lumière issue du soleil par de petits cristaux de glace en forme de bâtonnets. Les plus petits de ces cristaux (dont la taille peut être inférieure à 20 μm) ont un mouvement erratique provoqué par le choc des molécules qui constituent l’air ; ils ont donc toutes les orientations possibles dans l’espace. Puisqu’on ne s’intéresse qu’à la déviation des rayons lumineux, on peut modéliser la réfraction de la lumière issue du soleil par l’ensemble de ces cristaux par la réfraction de la lumière par un seul cristal en considérant un angle d’incidence variable.
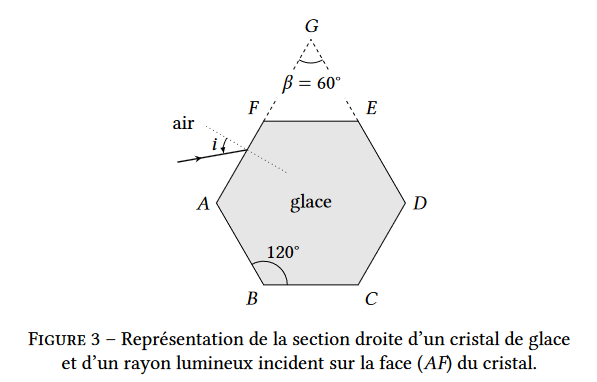
La figure 3 donne la représentation de la section droite d’un cristal de glace. Cette section présente la géométrie d’un hexagone régulier (𝐴𝐵𝐶𝐷𝐸𝐹). Un rayon lumineux incident, contenu dans le plan de cette section, atteint la face (𝐴𝐹 ) avec un angle d’incidence variable 𝑖. On étudie la déviation de ce rayon lumineux par le cristal.
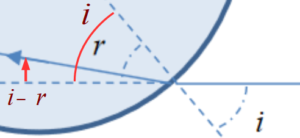
6. Justifier que le rayon lumineux qui émerge du cristal ne peut pas sortir par la face (𝐸𝐹).
On sait qu’il peut exister un angle limite $\theta_l$ pour le lequel le rayon dans la glace ne sortira pas(réflexion totale).
On peut alors légitimement se poser la question de la valeur de l’angle i, doit il être petit ou grand ?
Analysons le schéma suivant :
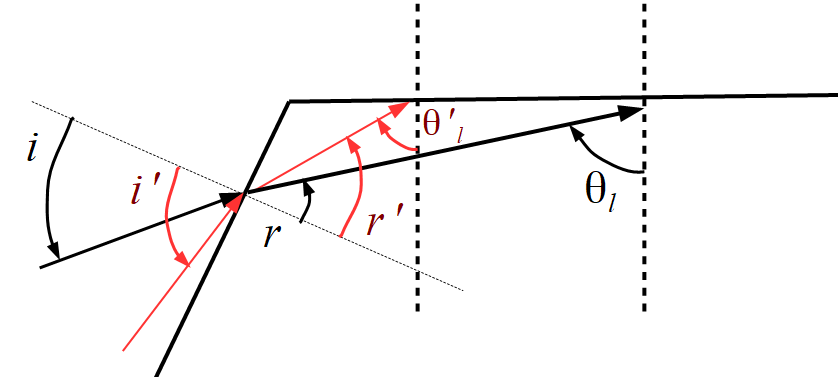
Si deux rayons entrent au même point avec $i’ > i$ alors $r’ > r$ car la fonction sinus est croissante sur l’intervalle $[0;\frac{\pi}{2}]$ et finalement $\theta_l > \theta_l’$
Or si on étudie le rayon qui donne un angle $\theta$ minimal et qu’il y a réflexion totale alors il n’est pas nécessaire d’étudier les angles $\theta_l$ supérieur car il y aura réflexion totale également.
Ici prendre l’angle $\theta_l$ le plus petit revient à prendre l’angle i le plus grand soit $\frac{\pi}{2}$
Pour retrouver la valeur de l’angle $\theta _{l,min}$ on utilise la propriété que dans un triangle, la somme des angles vaut 180°.
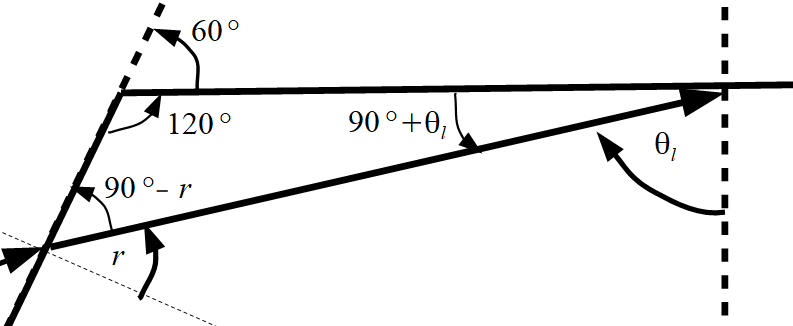
Attention ici à la convention du sens trigonométrique des angles. L’angle $\theta_l$ doit être négatif.
On retrouve :
$90-r+120+90 + \theta_l =180$
Soit $\theta_l = -120 + r$ avec $r=arcsin(\frac{n_a sin(\frac{\pi}{2})}{n_g})$
Application Numérique :
$\theta_l = -120 + arcsin(\frac{1 \times 1}{1,31})$ $= -70,2°$
L’angle limite est de -48,2°, on est donc bien au delà, il y a donc réflexion totale sur la face (EF)
7. Justifier qu’un rayon lumineux qui émerge par la face (𝐶𝐷) est parallèle au rayon lumineux incident et n’est donc pas dévié par le cristal de glace.
Traçons le parcours du rayon entrant en (AF) pour sortir en (CD) :
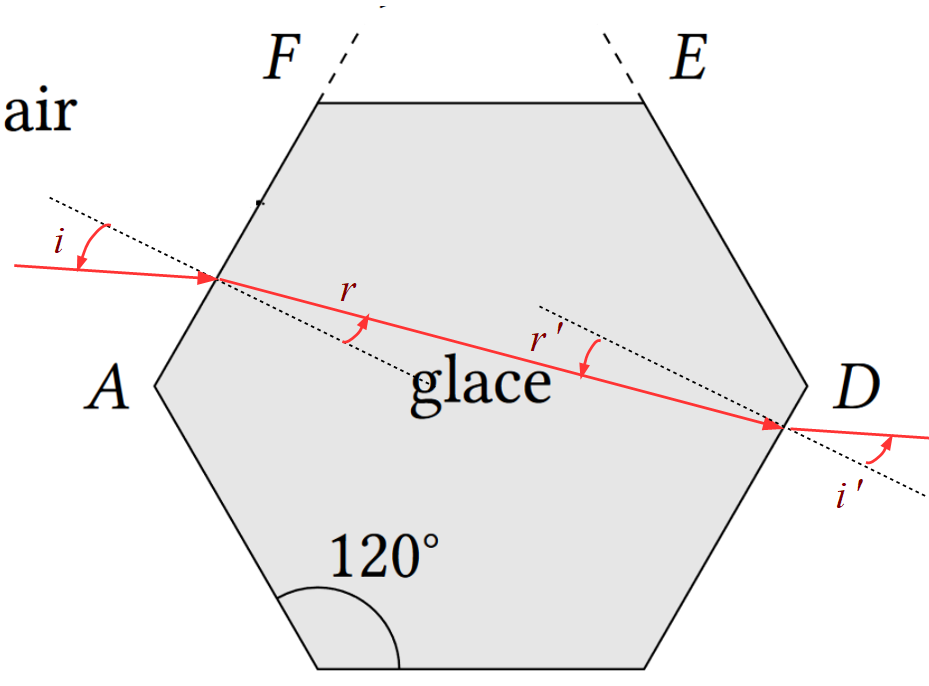
Les 2 faces (AF) et (CD) sont parallèles. Les normales à ces deux faces le sont également. Les angles r et r’ sont des angles alternes internes, ils sont donc égaux. r=r’.
Or à l’interface (AF) on a : $n_a sin(i) = n_g sin(r)$ et à l’interface (CD) on a : $n_g sin(r’) = n_a sin(i’)$
Comme $n_g sin(r) = n_g sin(r’)$ alors $n_a sin(i) = n_a sin(i’)$ soit $i=i’$
Le faisceau n’est donc pas dévié.
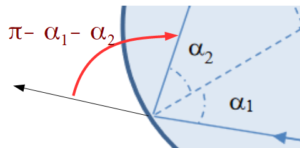
On considère le rayon émergent par la face (𝐷𝐸). Les faces (𝐴𝐹 ) et (𝐷𝐸) sont analogues aux faces d’un prisme de sommet 𝐺, d’angle au sommet 𝛽 égal à 60° et d’indice optique égal à celui de la glace, à savoir $𝑛_𝑔$ (voir figure 4).
Les différents angles sont définis sur la figure 4. On les oriente selon la convention suivante : les angles qui correspondent à une rotation dans le sens trigonométrique sont comptés positivement. Le sens trigonométrique est rappelé par une flèche courbe sur la figure 4, associée au symbole ⊕.
On note 𝛿 l’angle qui mesure la déviation du rayon incident après sa traversée du prisme. Les différents angles sur la figure 4 ont les signes suivants : 𝑖 > 0, 𝑟 > 0, 𝑖′ < 0, 𝑟′ < 0 et 𝛿 < 0.
8. Donner les relations qui lient 𝑖, 𝑟 et $𝑛_𝑔$ d’une part ; 𝑖′, 𝑟′ et $𝑛_𝑔$ d’autre part.
$sin(i) = n_g sin(r)$ car $n_a=1$
et
$n_g sin(r’) = sin(i’)$
9. Établir que : 𝛽 = 𝑟 − 𝑟′ et que 𝛿 = 𝑖 − 𝑟 + 𝑟′ − 𝑖′.
Pour $\beta$ :
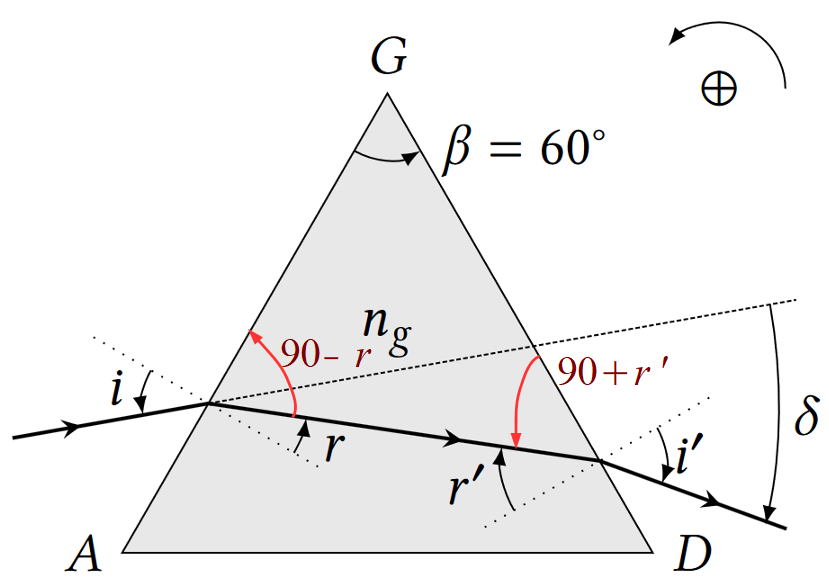
Attention au sens de l’angle, ici r’ est négatif. On retrouve un triangle dont la somme des angles vaut 180°.
$90 -r + \beta +90 +r’ = 180$ soit $\beta = r-r’$
Pour $\delta$ :
On observe déjà que $\delta$ est négatif. On peut décomposer la déviation en deux déviations $\delta_1 et \delta_2$.
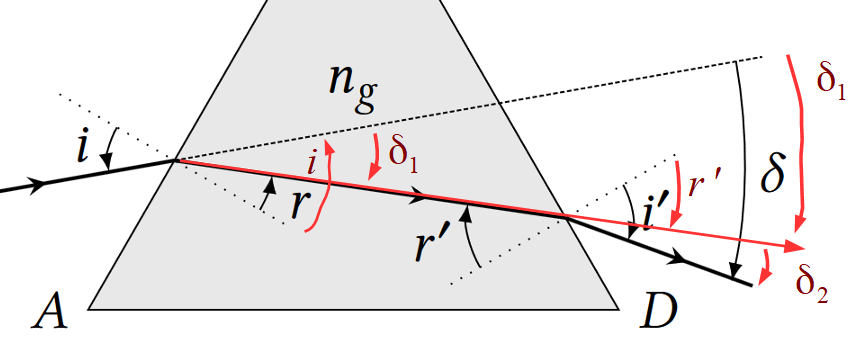
$\delta_1 = r-i <0$ et $\delta_2 = i’ – r’ <0 $
On a alors : $\delta = \delta_1 + \delta_2 $ $=r-i+i’-r’$
Ici il y a une erreur dans l’énoncé, on le voit particulièrement pour $\delta_1$, dans l’énoncé on nous propose $i-r$ or i et r sont tous les dans le sens positif et i>r ce qui donne $i-r>0$ pourtant on voit bien que sur le schéma $\delta_1 $ est négatif.
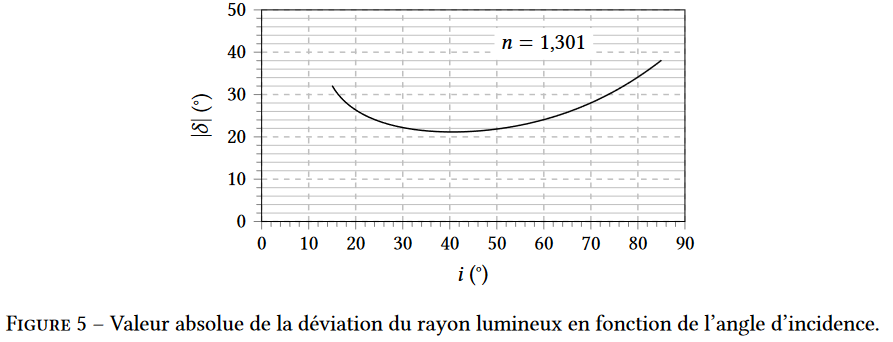
10. La figure 5 montre les variations de la valeur absolue de la déviation |𝛿| en fonction de l’angle d’incidence. On constate l’existence d’une valeur minimale dont on admet qu’elle est obtenue lorsque 𝑖 = −𝑖′. En déduire que dans cette configuration : 𝑟 = 𝛽/2 et $sin 𝑖 = 𝑛_𝑔 sin(𝛽/2)$ .
Si $i=-i’$ cela implique que $r=-r’$ donc $\beta = 2r$ $\Rightarrow r=\frac{\beta}{2}$
De plus, d’après la loi de Snell-Descartes : $n_a sin(i) = n_g sin(r)$ $\Rightarrow$ $sin(i) = n_g sin(\frac{\beta}{2})$
11. La figure 5 montre que la valeur minimale de |𝛿| est approximativement égale à 22°. Retrouver ce résultat par le calcul.
On a $r= \frac{\beta}{2} = 30°$ et $sin(i) = n_g sin(\frac{\beta}{2})$ donc $i= arcsin(n_g sin(\frac{\beta}{2})$
Application Numérique :
$i= arcsin(1,301 sin(\frac{60}{2}))$ $\simeq 41°$
On peut retrouver $\delta = 2i – 2r$
Application Numérique :
$\delta = 2 \times 41 – 2 \times 30$ $=22°$
12. Expliquer pourquoi l’observateur observe une accumulation de lumière (le halo solaire) dans la direction qui correspond à une ouverture angulaire de 22° autour de l’axe dirigé de son œil vers le Soleil.
Sur la figure 5, la déviation autour de 22° est obtenue pour une large gamme d’angle du rayon incident (i allant de 30° à 50°). La répartition de l’intensité lumineuse se fait alors plus importante dans cette direction.
13. L’indice optique de la glace est une fonction décroissante de la longueur d’onde. On observe que le halo solaire est irisé (l’irisation est la production des couleurs de l’arc-en-ciel par décomposition de la lumière du soleil) : de l’intérieur vers l’extérieur du halo, les couleurs observées varient du rouge au bleu. Préciser si les résultats établis précédemment sont en accord avec cette observation.
L’indice optique est une fonction décroissante de la longueur d’onde.
On a : $\lambda _{rouge}> \lambda_{bleu}$ $\Rightarrow$ $n_{rouge}<n_{bleu}$
Dans la glace, si $n_g$ augmente alors r diminue car $r=arcsin(\frac{sin(i)}{n_g})$ et arcsin est une fonction croissante, r varie en $arcsin(\frac{1}{r})$
Si r diminue alors r’ augmente car $\beta = r – r’ = 60°$
et si r’ augmente alors i’ augmente (Loi de Snell Descartes).
On en conclut que pour les indices élevés la déviation est plus grande, donc la déviation du bleu est plus importante que celle du rouge. La démonstration est en accord avec l’observation.
Extrait du sujet 2024 G2E voir le sujet corrigé complet
EXERCICE 4 : (extrait A BCPST 2023) Déviation lumière
D. DÉVIATION DE LA LUMIÈRE DANS UNE GOUTTE D’EAU
On cherche à calculer la déviation $𝐷$ d’un rayon lumineux provoquée par deux réflexions à l’intérieur d’une goutte d’eau (voir schéma ci-dessous). L’angle $𝐷$ est l’angle entre le rayon sortant et le rayon entrant dans la goutte. On constate une dispersion des rayons de la lumière blanche à l’intérieur de la goutte d’eau.
44. Rappeler les lois de Descartes de la réflexion et de la réfraction. On notera $𝑖$ l’angle d’incidence et $𝑏$ l’angle de réfraction (angles comptés positivement et non algébriques). On illustrera le propos par des schémas annotés
Réponse
Lois de Descartes :
Loi de la réflexion : Le rayon incident, la normale au dioptre et le rayon réfléchi sont contenus dans le même plan d’incidence. Les angles incidents $i$ et réfléchis $r’$ sont égaux en valeur absolus : $i = r’$
Loi de la réfraction : Le rayon incident, la normale au dioptre et le rayon réfléchi sont contenus dans le même plan d’incidence. La relation liant les indices de réfraction $n_1$ et $n_2$ de chacun des milieux et les angles incidents $i$ et réfracté $r$ s’écrit :
$n_1 sin(i) = n_2 sin(r)$
45. Préciser en quoi consiste la dispersion des rayons lumineux.
Réponse
La dispersion des rayons lumineux correspond aux changements de directions que peut prendre un rayon lumineux composé de plusieurs longueurs d’ondes différentes. L’angle de réfraction dépend de la longueur d’onde. Cela provient du fait que les ondes ne se déplacent pas à la même vitesse au sein d’un milieu dispersif.
46. Exprimer les angles $\alpha_j$ ($j = 1 à 6$ sur le schéma de la goutte) en fonction de $𝑖$ et de $r$.
Réponse
$\alpha_1 = r$, car on se trouve dans un triangle isocèle passant par O avec $\alpha_1 et r$ comme angle à la base et les 2 cotés égaux partant de O qui sont les rayons.
$\alpha_1$ et $\alpha_2$ sont égaux car il y a réflexion dans la goutte donc les angles sont égaux (loi de la réflexion)
$\alpha_2$ et $\alpha_3$ sont égaux (triangle isocèle)
$\alpha_3$ et $\alpha_4$ sont égaux(loi de la réflexion)
$\alpha_4$ et $\alpha_5$ sont égaux (triangle isocèle)
$\alpha_6 = i$ car on sort de la goutte en appliquant la loi de la réfraction avec comme angle incident $r$
Au final : $\alpha_1 = \alpha_2 = \alpha_3= \alpha_4= \alpha_5 =r$ ; $\alpha_6 = i$
47. Montrer que l’angle de déviation $𝐷$ s’écrit : $𝐷 = 2\pi + 2𝑖 – 6r$.
Réponse
On décompose les changements de directions depuis l’origine du rayon incident :
Une première déviation angulaire de $i-r$
Une deuxième déviation angulaire de $\pi – \alpha_1 – \alpha_2 = \pi – 2r$
Une troisième déviation angulaire de $\pi – \alpha_3 – \alpha_4 = \pi – 2r$
Une quatrième déviation équivalente à la première car on ressort de la goutte : $i-r$
La somme des déviations nous donne $D = i-r + \pi -2r + \pi -2r + i -r = 2\pi +2i -6r$
48. On se propose de déterminer numériquement la valeur de l’angle d’incidence $𝑖_𝑃$ telle que les rayons incidents et réfléchis par la goutte soient perpendiculaires. On constate par ailleurs que le minimum de déviation vaut $𝐷_{min} = 241°$. On utilise un programme Python utilisant la fonction $fsolve$. Compléter ce programme en donnant l’expression de la fonction f retenue, écrite en langage python. On prendra $𝑛_r = 1,3317$, l’indice de réfraction de l’eau pour une lumière rouge.
Données
La fonction fsolve du module scipy.optimize permet la résolution d’une équation de la forme f(x) = 0. Elle nécessite l’importation du module correspondant. La fonction f doit être définie au préalable et la valeur initiale $x_0$ de l ‘algorithme doit être précisée (valeur initiale à partir de laquelle le module recherche le zéro de la fonction). Syntaxe à utiliser :
import scipy.optimize as op
op.fsolve(f,x0)
np.arcsin(x) donne en radians la valeurs de l’angle x, compris entre -π/2 et π/2, dont on connaît le sinus.
math.degrees(a) donne la valeur de l’angle a en degrés à partir de sa valeur en radians
Programme python à compléter
import scipy.optimize as op
import numpy as np
import math
Pi = math.pi
def f(x) :
return À COMPLÉTER
x0 = 0
zero = op.fsolve(f,x0)
iP = math.degrees(zero)
print(« La valeur de iP recherchée en degrés proche de « ,x0, » est « ,iP , » »)
L’exécution du programme donne :
La valeur de iP recherchée en degrés, proche de 0, est 38.39
Réponse
La déviation est de $\frac{3 \pi}{2}$ pour que les rayons incident et réfléchis forment un angle droit.
La déviation est donnée par :
$D =2\pi +2i -6r = 2\pi +2i -6(arcsin(\frac{sin(i)}{1,3317}))$
La fonction op.solve permet de trouver la solution à une équation pour laquelle $f(x)=0$, or nous souhaitons trouver la solution pour $D = \frac{3 \pi}{2}$ . Il faut donc rechercher la solution pour $D – \frac{3 \pi}{2} = 0$
La ligne à ajouter dans la fonction est :
return 2*Pi + 2*x – 6*(np.arcsin(np.sin(x)/1.3317)) – 3*Pi/2
